阅读下列说明，回答问题1至问题2，将解答填入答题纸的对应栏内。【说明】0—1背包问题可以描述为：有n个物品，对i=l，2，…，n，第i个物品价值为vi，重量为wi(vi和wi为非负数)，背包容量为w(W为非负数)，选择其中一些物品装入背包，使装入背包物品的总价值最大，即，且总重量不超过背包容量，即，其中，xi∈{O，1}，xi=0表示第i个物品不放入背包，xi=1表示第i个物品放入背包。用回溯法求解此0—1背包问题，请填充下面伪代码中(1)～(4)处空缺。回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点已经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOuND(v，w，k，W)函数，其中v、w、k和w分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。下面给出0—1背包问题的回溯算法伪代码。函数参数说明如下：w：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。变量说明如下：cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。BKNAP(W，n，w，v，fw，fp，X)1 cw←cp02 (1)3 fp←l4 while true5 while k≤n and cw+w[k]≤w d。6 (2)7 cp←cp+v[k]8 Y[k]←l9 k←k+110 if kn then11 if fpcp then12 fp←cp13 fw←cw14 k←n15 X←Y16 else Y (k)←O17 while BOUND(cp，cw，k，W) ≤fp do18 while k≠O and Y(k)≠l d019 (3)20 if k=0 then return2l Y[k]←022 cw←cw-w[k]23 cp←cp-v[k]24 (4)
阅读下列说明，回答问题1至问题2，将解答填入答题纸的对应栏内。
【说明】
0—1背包问题可以描述为：有n个物品，对i=l，2，…，n，第i个物品价值为vi，重量为wi(vi和wi为非负数)，背包容量为w(W为非负数)，选择其中一些物品装入背包，使装入背包物品的总价值最大，即
，且总重量不超过背包容量，即
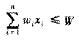，其中，xi∈{O，1}，xi=0表示第i个物品不放入背包，xi=1表示第i个物品放入背包。
用回溯法求解此0—1背包问题，请填充下面伪代码中(1)～(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点已经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOuND(v，w，k，W)函数，其中v、w、k和w分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。下面给出0—1背包问题的回溯算法伪代码。
函数参数说明如下：w：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。
变量说明如下：
cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。
BKNAP(W，n，w，v，fw，fp，X)
1 cw←cp0
2 (1)
3 fp←l
4 while true
5 while k≤n and cw+w[k]≤w d。
6 (2)
7 cp←cp+v[k]
8 Y[k]←l
9 k←k+1
10 if k>n then
11 if fp<cp then
12 fp←cp
13 fw←cw
14 k←n
15 X←Y
16 else Y (k)←O
17 while BOUND(cp，cw，k，W) ≤fp do
18 while k≠O and Y(k)≠l d0
19 (3)
20 if k=0 then return
2l Y[k]←0
22 cw←cw-w[k]
23 cp←cp-v[k]
24 (4)
相关考题：
0-1背包问题可以描述为：有n个物品，对i=1，2，…，n，第i个物品价值为vi ，重量为wi（vi，和wi为非负数），背包容量为W（W为非负数），选择其中一些物品装入背包，使装入背包物品的总价值最大，，且总重量不超过背包容量，即，其中，xi∈{0,1}，xi=0表示第i个物品不放入背包，xi=1表示第i个物品 放入背包。【问题1】（8分）用回溯法求解此0-1背包问题，请填充下面伪代码中（1）~（4）处空缺。回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点己经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND（v,w,k,W）函数，其中v, w, k和W分别表示当前已经获得的价值、当前背包的重量、己经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。下面给出0-1背包问题的回溯算法伪代码。函数参数说明如下：W：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。变量说明如下：cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。BKNAP(W,n,w,v,fw,fp,X）1 cw ← cp ← 02 （1）3 fp ← -14 while true5 while k≤n and cw＋w[k]≤W do6 （2）7 cp ← cp＋v[k]8 Y[k]← 19 k ← k+110 if k＞n then11 if fp＜cp then12 fp ← cp13 fw ← ew14 k ← n15 X ← Y16 else Y(k)← 017 while BOUND(cp,cw,k,W) ≤fp do18 while k≠0 and Y(k)≠1 do19 （3）20 if k＝0 then return21 Y[k]←022 cw ← cw ← w[k]23 cp ← cp ← v[k]24 （4）
背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=60；W2=20，V2=40；W3=20，V3=40；C=110。下列说法不正确的是（）A．利用价值密度最大的贪婪准则时，选物品1，这种方案的总价值为60B．最优解选物品为2和3，总价值为80C．使用贪婪准则，能保证得到最优解D．利用价值密度最大的贪婪准则时，选物品2和3，总价值为80
0-1背包问题：给定n种物品和一个背包。物品i的重量是Wi，其价值为Vi，背包的容量为C。应如何选择装入背包的物品，使得装入背包中物品的总价值最大？ 在选择装入背包的物品时，对每种物品i只有2种选择，即装入背包或不装入背包。不能将物品i装入背包多次，也不能只装入部分的物品i。用动态规划法编写算法和程序实现0-1背包问题。并给出如下测试用例的求解过程：有5件物品，重量分别为（3，2，1，4，5）,价值分别为（25,20,15,40,50)，背包容量w=6。
背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=60；W2=20，V2=40；W3=20，V3=40；C=110。下列说法不正确的是（）A．利用价值密度最大的贪婪准则时，选物品1，这种方案的总价值为60B．最优解选物品为2和3，总价值为80C．就本题而言，使用贪婪准则，能保证得到最优解D．利用价值密度最大的贪婪准则时，选物品2和3，总价值为80
背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择价值最大的物品装包。假设n=3；W1=100，V1=50；W2=20，V2=30；W3=20，V3=40；C=110。下列说法正确的是（）A．选物品1，这种方案的总价值为50B．选物品2和3，总价值为70C．使用贪婪准则，能保证得到最优解D．选物品1和3，总价值为90
133、背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=50；W2=20，V2=30；W3=20，V3=40；C=110。下列说法正确的是（）A．选物品1，这种方案的总价值为50B．选物品2和3，总价值为70C．使用贪婪准则，不能保证得到最优解D．选物品1和3，总价值为90
背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=50；W2=20，V2=30；W3=20，V3=40；C=110。下列说法正确的是（）A．选物品1，这种方案的总价值为50B．选物品2和3，总价值为70C．使用贪婪准则，不能保证得到最优解D．选物品1和3，总价值为90
背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=50；W2=20，V2=30；W3=20，V3=40；C=110。下列说法正确的是 （）A．选物品1，这种方案的总价值为50B．选物品为2和3，总价值为70C．使用贪婪准则，不能保证得到最优解D．选物品1和3，总价值为90
26、背包问题就是给定n种物品和一个背包，设Wi为物品i的重量，Vi为其价值，C为背包的重量容量，要求在重量容量的限制下，尽可能使装入的物品总价最大。用贪婪算法解决背包问题，贪婪准则为：每次都选择Vi/Wi 值（价值密度）最大的物品装包。假设n=3；W1=100，V1=50；W2=20，V2=30；W3=20，V3=40；C=110。下列说法正确的是 （）A．选物品1，这种方案的总价值为50B．选物品为2和3，总价值为70C．使用贪婪准则，不能保证得到最优解D．选物品1和3，总价值为90