m为收入,P1,P2分别为商品1和2的价格,当m>P2时,商品1和商品2的需求方程分别为X1 =假设横轴表示商品1的数量,纵轴表示商品2的数量,p1=1,P2 =2,当m>2时,收入提供曲线为( )。A.一条垂直线B.一条水平线C.一条斜率为2的直线D.一条斜率为1/2的直线
m为收入,P1,P2分别为商品1和2的价格,当m>P2时,商品1和商品2的需求方程分别为X1 =
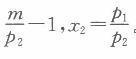
假设横轴表示商品1的数量,纵轴表示商品2的数量,p1=1,P2 =2,当m>2时,收入提供曲线为( )。
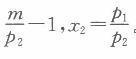
假设横轴表示商品1的数量,纵轴表示商品2的数量,p1=1,P2 =2,当m>2时,收入提供曲线为( )。
A.一条垂直线
B.一条水平线
C.一条斜率为2的直线
D.一条斜率为1/2的直线
B.一条水平线
C.一条斜率为2的直线
D.一条斜率为1/2的直线
参考解析
解析:在商品价格不变的情况下,当收入变化时,预算线平行移动会产生一连串的最优需求束,把这一连串的最优需求束连接起来的曲线就是收入提供曲线。p1=1,p2=2,当m>p:时,商品1、2的需求函数分别为

可知不论商品1如何随收入M变化,商品2的需求量固定,所以收入提供曲线为一条水平线。

可知不论商品1如何随收入M变化,商品2的需求量固定,所以收入提供曲线为一条水平线。
相关考题:
假设某投资连结保险的投保人选择了两个投资账户,投资单位数分别为X1和X2,投资单位价格分别为p1和p2,保单的账户价值为V,则下列正确的一项是()。A、V=X1×p1B、V=X2×p2C、V=X1+X2D、V=X1×p1+X2×p2
执行以下程序后,a,b的值分别为main(){ int a,b,k=4,m=6,*p1=k,*p2=m;a=p1==m;b=(*p1)/(*p2)+7;printf("a=%d\n",A.;printf("b=%d\n",B.;}A.-1,5B.1,6C.0,7D.4,10
假设某消费者的均衡如图所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点已知商品1的价格P1=2元。(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元,该消费者的效用函数为U=3X1X22,该消费者每年购买这两种商品的数量各应是多少?每年从中获得总效用是多少?
已知某消费者需求收入函数为Q=2000+0.2M,式中M代表收入,Q代表对某商品的需求量。试求:(1)M为10000元、15000元时对该商品的需求量;(2)当M=10000元和15000元时的需求收入弹性。
有以下程序include stcli0.hmain( ){ int a,b,k,m,*p1,*p2; k=1,m=8; p1=k,p2=stcli0.hmain( ){ int a,b,k,m,*p1,*p2;k=1,m=8;p1=k,p2=m;a=/*p1 -m; b=*p1+*p2+6;printf(”%d ”,a); printf(”%d\n”b);}编译时编译器提示错误信息,你认为出错的语句是A) a=/*p1- m;B)b=*p1+*p2+6;C)k=1,m=8;D)p1=k, p2=&m;
消费者显示了对于商品1和商品2的如下需求: 价格为(p1,p2)=(2,4)时,需求为(q1,q2)-(1,2);价格为(p1,p2)=(6,3)时,需求为(q1,q2)一(2,1)。该消费者的选择是与其效用最大化目标一致的。
设某消费者的效用函数为柯布-道格拉斯类型的,即U=x^αy^β,商品x和商品y的价格分别为Px和Py,消费者收入为M,α和β为常数切α+β=1 (1)求该消费者关于商品x和商品y的需求函数。 (2)证明:当商品x和y的价格及消费者的收入均以相同的比例变化时,消费者对两商品的需求关系维持不变; (3)证明:该消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。
己知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2= 30元,该消费者的效用函数为该消费者每年购买这两种商品的数量应各是多少每年从中获得的总效用是多少?
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 如果第一种商品价格由1提高为2,其他因素不变,则价格上升对第一种商品的消费量影响的总效应有多少?按照Slutsky分解原理,收入效应和替代效应分别是多少?
设某消费者的效用函数为柯布一道格拉斯类型的,即商品x和商品y的价格分别为消费者的收人为M,a和β为常数,且a+ β=1。 (1)求该消费者关于商品X和商品y的需求函数。 (2)证明当商品X和商品y的价格以及消费者的收入同时变动一个比例时,消费者对两商品的需求关系维持不变。 (3)证明消费者效用函数中的参数a和β分别为商品x和商品y的消费支出占消费者收入的份额。
某消费者的效用函数消费者的收人为M。 (1)请画出该消费者的无差异曲线。 (2)画出相应的收入消费曲线(ICC)、价格消费曲线(PCC)和恩格尔曲线(EC)。 (3)求商品X2的需求函数:X2 (Pl,P2,M)。 (4)已知M=100,求效用最大化的商品组合。
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 计算第一种商品价格从1变化为2,要保持原有效应不变的收入补偿数额。
已知某消费者的效用函数为U=X1X2,两商品的价格分别为P1=4、P2=2,消费者的收入是M=80.现在假定商品1的价格下降为P1=2.求: (1)由商品1的价格P1下降导致的总效应,使得该消费者对商品1的购买量发生多少变化? (2)由商品1的价格P1下降导致的替代效应,使得该消费者对商品1的购买量发生多少变化? (3)由商品1的价格P1下降导致的收入效应,使得该消费者对商品1的购买量发生多少变化?
某消费者的效用函数为u(x1.x2)一√五云,商品x1和x2的价格为P1和P2,收入为ya (1)假设商品x1和x2的价格为P1=l和P2=2,该消费者收入为y=100。求该消费者对两种商 品的需求量。 (2)若商品x1价格升至2,即此时P1=P2 =2,该消费者收入不变。求此价格变化对商品Xl产生的替代效应和收入效应。
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 消费者最优消费的xi和xo量。
假设消费者用既定的收入w购买两种商品,P1和P2分别为两种商品的既定价格,以Q1和Q2分别表示两种商品的数量,则P1Q1+P2Q2=w;MU1和MU2分别表示两种商品的边际效用,λ表示每一元货币带来的边际效用,则消费者效用最大化的均衡条件为( )。A.MU1/P2=MU2/P1=λB.MU1/P1=MU2/P2=λC.P1/MU1=P2/MU2=λD.P2/MU1=P1/MU2=λ
若有说明:int *p1,*p2,m=5,n; 以下都是正确的赋值语句的选项是()。A、p1=m; p2=p1;B、p1=m; p2=n; *p1=*p2;C、p1=m; p2=p1;D、p1=m; *p2=*p1;
若有说明:int*p1,*p2,m=5,n=9;以下均是正确赋值语句的选项是()A、p1=m;p2=p1;B、p1=m;p2=n;*p1=*p2;C、p1=m;p2=p1D、p1=m;*p2=*p1;
单选题若有说明:int *p1,*p2,m=5,n; 以下都是正确的赋值语句的选项是()。Ap1=m; p2=p1;Bp1=m; p2=n; *p1=*p2;Cp1=m; p2=p1;Dp1=m; *p2=*p1;