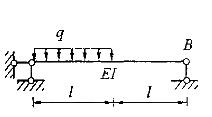
图示为梁在实际状态下的MP图,EI=常数,则K截面的角位移46.6/EI。()此题为判断题(对,错)。
图示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B端转角为:A.θ,顺时针B.θ,逆时针C.θ/2,顺时针D.θ/2,逆时针
图示结构杆长为l,EI=常数,C点两侧截面相对转角φC为:
图所示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
图示结构EI=常数,当支座A发生转角θ支座B处截面的转角为(以顺时针为正)( )。A.θ/3B.2θ/5C.-θ/3D.-2θ/5
图示连续梁,EI=常数,已知支承B处梁截面转角为-7Pl2/240EI(逆时针向),则支承C处梁截面转角φC应为:
图示梁AB,EI为常数,固支端A发生顺时针的支座转动,由此引起的B处的转角为( )。
图示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
图示连续梁,EI=常数,欲使支承B处梁截面的转角为零,比值a/b应为:
图示刚架EI=常数,截面C和D的相对转角为( )。
图示刚架,EI为常数,忽略轴向变形。当D支座发生支座沉降时,B点转角为( )。
图示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
图所示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B处的转角为( )。{图} A.θ,顺时针 B.θ,逆时针 C.θ/ 2,顺时针 D.θ/ 2,逆时针
图示连续梁,EI=常数,欲使支承B处梁截面的转角为零,比值a/b应为:A. 1/2B. 2C. 1/4D. 4
图示结构EI=常数,当支座B发生沉降Δ时,支座B处梁截面的转角为(以顺时针为正)( )。A、Δ/lB、1、2Δ/lC、1、5Δ/lD、Δ/2l
图示梁和常数,固定端A发生顺时针方向角位移θ,则铰支端B的转角(以顺时针方向为正)为:( )A.θ/2B.θC.-θ/2D.-θ
图示为结构在荷载作用下的M图,各杆EI=常数,则支座B处截面的转角为:
图示结构各杆EI=常数,其C端的水平位移(→)为:
已知图示梁抗弯刚度EI为常数,则用叠加法可得跨中点C的挠度为:
已知图示梁抗弯刚度EI为常数,则用叠加法可得自由端C点的挠度为:
用位移法计算图示连续梁,并绘出弯矩图。各杆EI相同且为常数。
有一简支梁,中点受集中力P作用。梁端转角θ=Pl2/16EI,当梁的长度l、横截面尺寸、荷载P均增大一倍时,梁端转角等于原转角的多少倍?()A、1/2B、1C、2D、4
单选题有一简支梁,中点受集中力P作用。梁端转角θ=Pl2/16EI,当梁的长度l、横截面尺寸、荷载P均增大一倍时,梁端转角等于原转角的多少倍?()A1/2B1C2D4
单选题图示结构,EI=常数,欲使结点B的转角为零,比值P1/P2应为:()A 1.5B 2C 2.5D 3