图所示对称刚架，不计轴向变形，弯矩图为（　　）。 A、两杆均内侧受拉 B、两杆均外侧受拉 C、两杆均部分内侧受拉 D、两杆弯矩都为零

图所示对称刚架，不计轴向变形，弯矩图为（　　）。


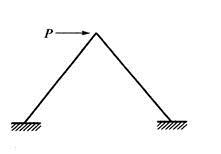
A、两杆均内侧受拉
B、两杆均外侧受拉
C、两杆均部分内侧受拉
D、两杆弯矩都为零

参考解析

解析：把荷载分解为正对称荷载和反对称荷载，正对称荷载下没有竖向位移，又因为轴向变形不考虑，也没有转角和水平位移，反对称情况下，反对称位移为零又因为轴向变形不考虑，也没有竖向，位移由位移法可知，节点因为没有线位移和角位移所以没有弯矩。

相关考题：

绘制平面刚架弯矩图时,受均布荷载作用,弯矩图的形状为()。 A、抛物线B、折线C、直线D、曲线
查看答案
荷载作用下的梁和刚架中,位移的主要贡献是弯曲变形,通常剪切变形和轴向变形可以忽略不计。() 此题为判断题(对，错)。
查看答案
悬臂梁受载如图所示，则其弯矩图为( )。
查看答案
图所示刚架中截面D的弯矩为（　　）。 A、Fpl/8，左边受拉 B、0 C、Fpl/8，右边受拉 D、Fpl/4，右边受拉
查看答案
忽略轴向变形时，图所示结构中，（EI＝常数）A端的弯矩MA等于（　　）。 A、0 B、2Fa/3（右侧受拉） C、Fa（左侧受拉） D、Fa（右侧受拉）
查看答案
已知图为刚架在荷载作用下的弯矩图，各柱顶的水平线位移ΔH之值为（　　）。
查看答案
已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
图所示对称结构，在不计杆件轴向变形的情况下，各结点线位移（　　）。 A、△l=△2=△3 B、△l=△2≠△3 C、△l≠△2≠△3 D、△l=△3≠△2
查看答案
图所示结构，忽略轴向变形，梁柱质量忽略不计。该结构动力自由度的个数为（　　）。 A、1 B、2 C、3 D、4
查看答案
图示对称结构，在不计杆件轴向变形的情况下，各结点线位移（　　）。
查看答案
图示对称刚架，不计轴向变形，弯矩图为（　　）。A、两杆均内侧受拉B、两杆均外侧受拉C、两杆均部分内侧受拉D、两杆弯矩都为零
查看答案
图示两刚架的EI均为常数，已知EIa=4EIb，则图a)刚架各截面弯矩与图b)刚架各相应截面弯矩的倍数关系为：
查看答案
图所示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念）
查看答案
图a)为对称刚架，具有两根对称轴，利用对称性简化后，正确的计算简图为图b)四个图中的:
查看答案
图刚架不计分布质量，则其自振频率为（　　）。
查看答案
左图所示对称刚架受同向结点力偶作用，弯矩图的正确形状是右侧四个图中的：
查看答案
图所示刚架的自振频率为（　　）。
查看答案
A.整个刚架无弯矩B.整个刚架都有弯矩C.横梁无弯矩，柱有弯矩D.横梁有弯矩，柱无弯矩
查看答案
某车间设备平台改造增加一跨，新增部分跨度8m，柱距6m，采用柱下端铰接、梁柱刚接、梁与原有平台铰接的刚架结构，平台铺板为钢格栅板；刚架计算简图如下图所示；图中长度单位为mm。刚架与支撑全部采用Q235-B钢，手工焊接采用E43型焊条。设计条件同题27，刚架柱上端的弯矩及轴向压力设计值分别为财M2=192.51ΚΝ.m，N=276ΚΝ.m刚架柱下端的弯矩及轴向压力设计值分别为；且无横向荷载作用。假设刚架柱在弯矩作用平面内计算长度取。试问，对刚架柱进行弯矩作用平面内整体稳定性验算时，以应力形式表达的稳定性计算数值（N/mm2）与下列何项数值最为接近？（A）134（B）156 （C）173（D）189
查看答案
下图所示刚架中，哪一个刚架的横梁跨中弯矩最大？( )A.B.C.D.
查看答案
用位移法求解刚架，并绘弯矩图。各杆EI相同等于常数。
查看答案
用位移法计算图示刚架，并绘制弯矩图。
查看答案
对称结构在对称载荷作用下，一定有（）。A、剪力图对称B、弯矩图对称C、剪力图和弯矩图都对称D、剪力图和弯矩图都反对称
查看答案
如果梁的外力（包括载荷及支座）为对称图形，则此梁的剪力图和弯矩图应当是（）。A、剪力图和弯矩图均为正对称图形B、剪力图为正对称图形，弯矩图为反对称图形C、剪力图和弯矩图均为反对称图形D、剪力图为反对称图形，弯矩图为正对称图形
查看答案
对称结构在反对称载荷作用下，一定有（）。A、剪力图对称B、弯矩图对称C、剪力图和弯矩图都对称D、剪力图和弯矩图都反对称
查看答案
单选题对称结构在对称载荷作用下，一定有（）。A剪力图对称B弯矩图对称C剪力图和弯矩图都对称D剪力图和弯矩图都反对称
查看答案
单选题对称结构在反对称载荷作用下，一定有（）。A剪力图对称B弯矩图对称C剪力图和弯矩图都对称D剪力图和弯矩图都反对称
查看答案
热门标签