忽略轴向变形时，图所示结构中，（EI＝常数）A端的弯矩MA等于（　　）。 A、0 B、2Fa/3（右侧受拉） C、Fa（左侧受拉） D、Fa（右侧受拉）

忽略轴向变形时，图所示结构中，（EI＝常数）A端的弯矩MA等于（　　）。


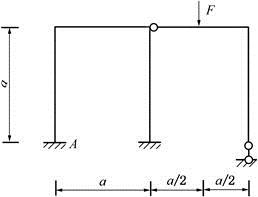
A、0
B、2Fa/3（右侧受拉）
C、Fa（左侧受拉）
D、Fa（右侧受拉）

参考解析

解析：由右侧静定结构受力平衡可知，作用在左侧超静定刚架上的荷载竖直向下，由于刚架各杆忽略轴向变形的影响，图示荷载在左侧结构中不会引起任何结点线位移，故A端的弯矩为零。

相关考题：

图示结构EI=常数，截面A右侧的弯矩为()A.M/2B.MC.0D.M/(2EI)
查看答案
图所示的刚架，EI＝常数，各杆长为l，A截面的转角为（　　）。
查看答案
图示结构EI＝常数，不考虑轴向变形，FQBA为（　　）。A． P/4B． －P/4C． P/2D． －P/2
查看答案
图示结构EI＝常数，不考虑轴向变形，MBA为（以下侧受拉为正）（　　）。
查看答案
已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
图所示刚架，EI=常数，结点A的转角是（　　）。（提示：利用转动刚度的概念）
查看答案
结构在荷载下的弯矩图如图所示，曲线为q＝2kN／m引起的二次抛物线，EI＝常数。B点的水平位移为（　　）。A．108／（EI）（→）B．756／（EI）（→）C．828／（EI）（→）D．900／（EI）（→）
查看答案
图示结构(不计轴向变形)AB杆轴力为(EI=常数)：
查看答案
如图所示的结构，EI＝常数，杆端弯矩（顺时针为正）正确的是（　　）。
查看答案
图所示结构，忽略轴向变形，梁柱质量忽略不计。该结构动力自由度的个数为（　　）。 A、1 B、2 C、3 D、4
查看答案
图所示结构EI为常数，用力矩分配法求得弯矩Mba是（　　）。 A、2kN·m B、-2kN·m C、8kN·m D、-8kN·m
查看答案
图示刚架，EI为常数，忽略轴向变形。当D支座发生支座沉降时，B点转角为（　　）。
查看答案
如图所示的结构（EI＝常数）中，D点水平位移（向右为正）为（　　）。
查看答案
图示两刚架的EI均为常数，已知EIa=4EIb，则图a)刚架各截面弯矩与图b)刚架各相应截面弯矩的倍数关系为：
查看答案
图示结构EI=常数，A点右侧截面的弯矩为：
查看答案
图所示结构，EI=常数，截面高h=常数，线膨胀系数为α，外侧环境温度降低t℃，内侧环境温度升高t℃，引起的C点竖向位移大小为（　　）。
查看答案
图所示结构（E为常数），杆端弯矩（顺时针为正）正确的一组为（　　）。
查看答案
用力法求解图所示结构（EI=常数），基本体系及基本未知量如图所示，力法方程中的系数为（　　）。
查看答案
图示结构（忽略轴向变形的影响）BD杆的M、Q特征为（　　）。A．M≠0；Q＝常数B．M＝常数；Q＝0C．M＝0；Q＝0D．MBD＝0；Q＝常数
查看答案
用位移法计算图所示梁（EI=常数），基本体系如图所示，k11为（　　）。 A、6EI/l B、7EI/l C、8EI/l D、9EI/l
查看答案
如图a)所示结构，取图b)为力法基本体系，EI=常数，Δ1P为:
查看答案
图示结构各杆EI=常数，杆端弯矩MDE:
查看答案
用位移法计算图示连续梁，并绘出弯矩图。各杆EI相同且为常数。
查看答案
用力矩分配法计算图示结构，并绘出弯矩图。各杆EI相同且为常数。
查看答案
用力法计算图示结构，并作弯矩图。各杆EI相同且为常数。
查看答案
图示结构中，除横梁外，各杆件EI=常数。不考虑杆件的轴向变形，则体系振动的自由度数为1 A对B错
查看答案
用位移法求解刚架，并绘弯矩图。各杆EI相同等于常数。
查看答案
热门标签