纯交换的完全竞争市场上两个消费者A和B,两种商品X,Y,消费者A和B的效用函数分别为U(XA,YA)一XAYA和U(XB,YB)一In XB +αln YB。其中,(XA,YA)分别为消费者A在X,Y上的消费,(XB,YB)同理。A和B的初始禀赋分别为(eAX,eAY),(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)},(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)}。求竞争性市场均衡条件下的产品价格以及每个消费者的情况。求竞争性市场均衡条件下的产品价格以及每个消费者的情况。
纯交换的完全竞争市场上两个消费者A和B,两种商品X,Y,消费者A和B的效用函数分别为U(XA,YA)一XAYA和U(XB,YB)一In XB +αln YB。其中,(XA,YA)分别为消费者A在X,Y上的消费,(XB,YB)同理。A和B的初始禀赋分别为(eAX,eAY),(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)},(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)}。求竞争性市场均衡条件下的产品价格以及每个消费者的情况。求竞争性市场均衡条件下的产品价格以及每个消费者的情况。
参考解析
解析:不妨设商品X的价格为1,商品Y的相对价格为p。 消费者A的问题为:
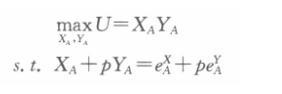
构造拉格朗日辅助函数L(XA,YA,λ)=XAYA +λ(eXA十peYA-XA -pYA),一阶条件为:
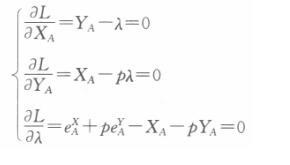
解得消费者A对X和Y的需求函数分别是 同理可以解得消费者B对X和Y的需求函数分别是
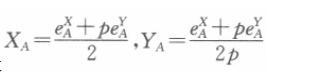
同理可以解得消费者B对X和Y的需求函数分别是
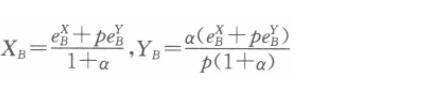
市场均衡条件下,有
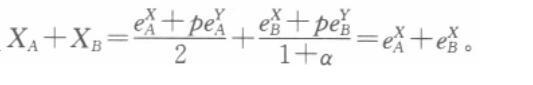
解得:
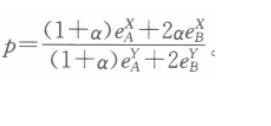
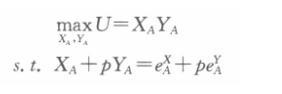
构造拉格朗日辅助函数L(XA,YA,λ)=XAYA +λ(eXA十peYA-XA -pYA),一阶条件为:
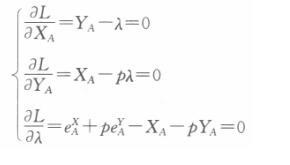
解得消费者A对X和Y的需求函数分别是 同理可以解得消费者B对X和Y的需求函数分别是
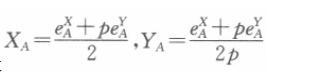
同理可以解得消费者B对X和Y的需求函数分别是
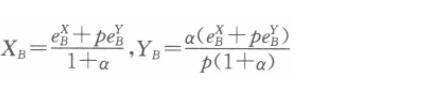
市场均衡条件下,有
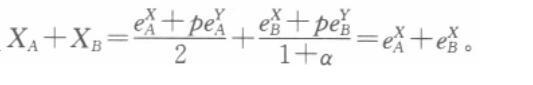
解得:
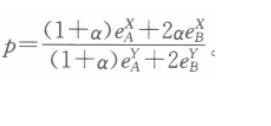
相关考题:
有如下类声明: class XA{ int X; public: XA(int n){x=n;} }; class XB:public XA{ int y; public: XB(int a,int b); }; 在构造函数XB的下列定义中,正确的是( )。A.XB::XB(inta,int b):x(a),y(b){}B.XB::XB(int a,int b):XA(a),y(b){}C.XB::XB(int a,int b):x(a),XB(b){}D.XB::XB(int a,int b):XA(a),XB(b){}
有如下类声明:class XA{int x;public:XA(int U)}x=n;}};class XB:public XA{int y;public:XB(int a,int B) ;};在构造函数XB的下列定义中,正确的是A.XB::XB(int a,int B) :x(A) ,y(B) {}B.XB::xB(int a,int B) :XA(A) ,y(B) {}C.XB::XB(int a,int B) :x(A) ,XB(B) {}D.XB::XB(int a,int B) :XA(A) ,XB(B) {}
有如下类声明: class XA { int x; public: XA(int n) {x=n;} }; class XB: public XA{ int y; public: XB(int a,int b); };在构造函数XB的下列定义中,正确的是______。A.XB:: XB(int a, int b):x(a),y(b) { }B.XB::XB(int a, int b):XA(a),y(b){}C.XB::XB(int a,int b):x(a),XB(b)i}D.XB::XB(int a,int b):XA(a),XB(b){}
纯交换的完全竞争市场上两个消费者A和B,两种商品X,Y,消费者A和B的效用函数分别为U(XA,YA)一XAYA和U(XB,YB)一In XB +αln YB。其中,(XA,YA)分别为消费者A在X,Y上的消费,(XB,YB)同理。A和B的初始禀赋分别为(eAX,eAY),(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)}。交易后,人们的效用水平上升了还是下降了?为什么?
设a、b两个消费者消费x、y两种产品:两个消费者的效用函数均为u=xy -消费者a消费的x和y的数量分别用xa和ya表示,消费者6消费的x和v的数量分别用Xb和Yb表示.e(xa=1O,ya=50,xb=90,yb=270)是相应的埃奇渥斯盒状图中的一点: (1)试确定:在点e处,消费者a的边际替代率。 (2)试确定:在点e处,消费者b的边际替代率。 (3)点e满足交换的帕累托最优吗? (4)如果不满足,应如何调整才符合帕累托改进的要求?
纯交换的完全竞争市场上两个消费者A和B,两种商品X,Y,消费者A和B的效用函数分别为U(XA,YA)一XAYA和U(XB,YB)一In XB +αln YB。其中,(XA,YA)分别为消费者A在X,Y上的消费,(XB,YB)同理。A和B的初始禀赋分别为(eAX,eAY),(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)}。给定初始禀赋不变,试分别考虑在α=l,α≠1情况下,通过以下方法改变两个消费者的初始禀赋分配情况:把商品X或Y从A的初始禀赋挪到B的初始禀赋中,会对市场均衡价格有何影响?市场总需求跟初始的禀赋分配状况相关吗?为什么?
假定小王(A)和小李(B)的效用函数分别为U.4 =xAyA,UB=XB +yB。 (1)请针对两人分别写出x对y的边际替代率公式。 (2)如果交易通过价格体系来实施,请写出均衡时的(可行的)价格比率。 (3)假定共有100单位的x和200单位的y。最初,小王有25单位的x和75单位的y,而小李有75单位的x和125单位的y。请说明经过市场交易后,均衡时两人分别拥有的两种商品的数量。 (4)画出这种情形的埃奇沃斯框图,标出初始禀赋配置和所有的帕累托最优配置。
设某消费者的效用函数为柯布-道格拉斯类型的,即U=x^αy^β,商品x和商品y的价格分别为Px和Py,消费者收入为M,α和β为常数切α+β=1 (1)求该消费者关于商品x和商品y的需求函数。 (2)证明:当商品x和y的价格及消费者的收入均以相同的比例变化时,消费者对两商品的需求关系维持不变; (3)证明:该消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。
纯交换的完全竞争市场上两个消费者A和B,两种商品X,Y,消费者A和B的效用函数分别为U(XA,YA)一XAYA和U(XB,YB)一In XB +αln YB。其中,(XA,YA)分别为消费者A在X,Y上的消费,(XB,YB)同理。A和B的初始禀赋分别为(eAX,eAY),(eBx,eBY)。经济体的初始总禀赋为(EX,EY)一{(eAX+eBx),(eAY+eBY)}。(5)A的效用函数变成U(XA,YA)=βln XA +βln YA。那么(1)~(4)的答案是否会发生变化?为 什么?
假设在一个2×2的交换经济中消费者A和B交换两种商品z和y,消费者A的效用函数 是UA (XA,yA)=,消费者B的效用函数是ub(xb,yB)=他们拥有两种商品的初始 禀赋分别是WA(40,60)和WB(40,40)。标准化商品x的价格Px=1,商品y的价格为P。 (1)计算消费者A和B对两种商品z和y的需求函数。 (2)计算该交换经济的均衡价格及均衡配置。
在地形图上,量得A、B两点的坐标分别为xA=1630.744m,yA=834.560m,xB=1278.330m,yB=1408.885m,则观测边长为()m。A、796.184B、130.555C、806.817D、673.828
在地形图上,量得A、B两点的坐标分别为xA=2910.14m,yA=3133.78m,xB=3110.14m,yB=2933.78m,则AB的坐标方位角为()A、45°B、135°C、225°D、315°
在地形图上,量得A、B的坐标分别为xA=432.87m,yA=432.87m,xB=300.23m,yB=300.23m,则AB的方位角为()。A、315°B、225°C、150°D、300°
在地形图上,量得A、B的坐标分别为xA=432.87m,yA=432.87m,xB=300.23m,yB=300.23m,则AB的边长为()m。A、187.58B、733.10C、132.64D、1257.12
单选题在地形图上,量得A、B的坐标分别为xA=432.87m,yA=432.87m,xB=300.23m,yB=300.23m,则AB的边长为()m。A187.58B733.10C132.64D1257.12
填空题已知A、B两点的坐标值分别为xA=5773.633m,yA=4244.098m,xB=6190.496m,yB=4193.614m,则坐标方位角αAB=()、水平距离DAB=()m。