竞争性市场下有3个完全相同的企业,生产相同产品。市场的反需求曲线为p(Q)-l-Q,Q=q1+q2+q3,每个企业成本为零。若其中两个公司合并,企业各自的利润分别是多少?
竞争性市场下有3个完全相同的企业,生产相同产品。市场的反需求曲线为p(Q)-l-Q,Q=q1+q2+q3,每个企业成本为零。若其中两个公司合并,企业各自的利润分别是多少?
参考解析
解析:不妨设企业1和2合并为企业4,那么企业4的利润函数为π4=p4q4=(1- q3 - q4)q4,利润最大化的一阶条件为:
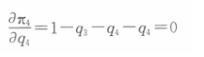
得厂商4的反应函数为
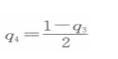
同理可得厂商3的反应函数为

联立两个反应函数,得到古诺均衡解为
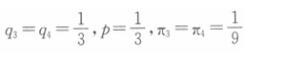
若企业1和2平分利润,则
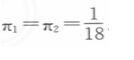
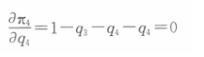
得厂商4的反应函数为
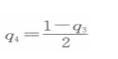
同理可得厂商3的反应函数为

联立两个反应函数,得到古诺均衡解为
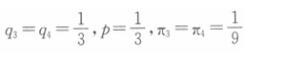
若企业1和2平分利润,则
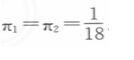
相关考题:
假设某市场仅有两个企业,它们面临共同的市场需求曲线P=15Q,两个企业的成本函数分别为C1=5Q1,5Q22,且两个勾结成卡特尔,则两企业产量为().A.Q1=90,Q2=10B.Q1=80,Q2=10C.Q1=80,Q2=5D.Q1=90,Q2=5
已知某企业的成本函数为C=q2+100,C为总成本,q为产量,试问:(1)若产品市场价格p=40,那么产量为多少才可实现最大利润?(2)当产品市场价格达到多少时,该企业才会获得正的市场利润?
某产品的市场需求曲线为Q=2O -P,市场中有n个生产成本相同的厂商,单个厂商的成本函数为c=2q2+2,问: (1)若该市场为竞争性市场,市场均衡时的市场价格和单个企业的产量是多少? (2)长期均衡时该市场中最多有多少个厂商? (3)若该市场为寡头垄断市场,古诺均衡时的市场价格和单个企业的产量是多少?
假设在一个市场上有两家企业,该市场的逆需求函数为P=4一罢,企业1的成本函数为 c1= q1,企业2的成本函数为C2 =2q2,P为价格,Q为两个企业的总产量,q为每个企业的产量。 (1)假设两个企业可以组成一个卡特尔,求垄断价格及每个企业的产量。 (2)试证明:卡特尔不是一个纳什均衡。 (3)假设两个企业进行产量竞争,求古诺均衡下的价格和每个企业的产量。
甲企业的产品在市场上占据垄断地位,该企业有两个工厂都能生产这种产品,其成本函数为Cl=3+2Q1+5Q12,C2=5+30Q2 +Q22。甲企业估计其短期面临的产品需求曲线为P=30-2(Q1+ Q2),请问:甲企业在各个工厂应该生产多少?其将获得多少利润?
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 若各企业合并为一家,新的产量和利润为多少,并比较与第一问结果的区别。
已知市场上有N家成本一样的企业,单个厂商长期总成本函数为整个市场的需求曲线为Q=20-2p。 (1)若市场为垄断竞争市场,且每家企业的需求为整个市场需求的1/N,请问当N等于8时,此时市场是否处于长期均衡,为什么? (2)如果该市场为完全竞争市场,那么长期均衡时市场上企业的数量N是多少?
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商的生产均面临不变的边际成本1/2,且反需求曲线为p=1-Q,则均衡时两个企业的产量分别是多少?
一个垄断厂商生产某种产品的成本函数为:C=5+3Q,将其产品在两个地理分割的市场上销售,这两个市场对该产品的需求函数分别为:P1=15-Q1,P2=25-2Q2。 假设企业被禁止使用价格歧视策略,那么该企业将采取何种价格策略?能够在两个市场各自销售多少产品?两个市场总共实现多少利润?在两个市场上分别造成多少福利损失?
一个垄断厂商生产某种产品的成本函数为:C=5+3Q,将其产品在两个地理分割的市场上销售,这两个市场对该产品的需求函数分别为:P1=15-Q1,P2=25-2Q2。 该垄断厂商将针对两个市场制定何种价格策略?两个市场各自能够销售多少产品?厂商实现多少总利润?在两个市场分别造成多少福利损失?
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时候企业个数
竞争性市场下有3个完全相同的企业,生产相同产品。市场的反需求曲线为p(Q)-l-Q,Q=q1+q2+q3,每个企业成本为零。若他们可以生产类似但不完全相同的产品,那么两个公司合并是否有利可图?为什么?
某市场存在两家企业A和B,该市场的需求函数为P=100—ql一q2,其中q1和q2分别表示两家企业所销售的数量,如果这两家企业进行产量竞争,其边际成本都为20,并且没有固定的成本。(1)假设这两家企业同时选择产量,请计算两家企业各自的均衡产量。(2)若这两家企业合并为一家企业,请计算均衡产量。
考虑以下古诺竞争模型。市场中有N个企业,生产相同的产品,均没有生产成本。市场需求函数为P=a-bQ,其中a,b>0,Q为行业总产量。如果企业同时展开产量竞争,那么: (1)均衡时价格是多少? (2)此时消费者剩余是多少?
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时的单个企业产量和价格
A企业生产矿泉水,其所在的市场为完全竞争市场。A的短期成本函数为C(q)=20+5q十q2,其中20为企业的固定成本。 (1)请推导出A企业的短期供给曲线。 (2)当市场价格为15时,短期均衡的利润为多少?此时的生产者剩余是多少? (3)若产量大于0时,长期成本函数C(q) =9+4q+q2,则长期均衡的产出是多少?长期均衡的利润为多少?
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 假设价格为P,求N个企业进行古诺竞争时每个企业的产量和利润,以及市场总产量和总利润。
一个市场的需求函数为:P(Q)=100-2Q,企业的成本函数为:C(Q)=4Q,下列说法正确的有()。Ⅰ.若该市场为完全竞争市场,则均衡价格P=4,均衡产量为48Ⅱ.当市场上有2个企业时,若处于古诺均衡,则均衡价格是36Ⅲ.当市场上有2个企业时,若处于斯塔克尔伯格均衡,则均衡价格为36Ⅳ.当市场上有2个企业时,若达成卡特尔均衡,则两个企业都没有违约动机A.Ⅰ、ⅡB.Ⅰ、ⅢC.Ⅲ、ⅣD.Ⅰ、Ⅱ、Ⅳ
已知某完全垄断企业的需求函数为P=17-4Q,成本函数为TC=5Q+2Q2。 (1)计算企业利润最大化的价格和产出、利润。 (2)如果政府实行价格管制,按边际成本定价与按平均成本定价,价格分别是多少?厂商是否亏损?
单选题假设某市场仅有两个企业,它们面临共同的市场需求曲线P=15Q,两个企业的成本函数分别为C1=5Q1,5Q22,且两个勾结成卡特尔,则两企业产量为().AQ1=90,Q2=10BQ1=80,Q2=10CQ1=80,Q2=5DQ1=90,Q2=5
问答题若垄断企业的成本函数为C=6Q+0.O5Q2,产品的需求函数为Q=360-20P。 (1)计算垄断企业最大利润及相应的产量和价格; (2)若政府限定最高售价为13元,此时垄断企业会提供多少产品?能得到多少利润?市场会出现短缺吗?
问答题某垄断者的产品在两个分割市场出售,产品的成本函数和两个市场的需求函数分别为TC=Q2+10Q,Q1=32-0.4P1,Q2=18-0.1P2,其中Q=Q1+Q2。 (1)假设两个市场能实行差别价格,求解利润最大时的两个市场的售价、销售量和利润。 (2)假设两个市场只能索取相同价格,求解利润最大时的售价、销售量和利润。
问答题假设市场中有大量企业,每家企业的长期生产函数都相同,为LC=Q3-4Q2+8Q。 (1)试求该市场达到长期均衡的价格; (2)如果市场需求函数为Q=2000-1OOP,在市场达到长期均衡时,市场交易量是多少?市场中容纳了多少家企业?