下图是从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，则不可能相对的两个面是（ ）。A.1和6B.2和5C.3和4D.4和5

下图是从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，则不可能相对的两个面是（ ）。

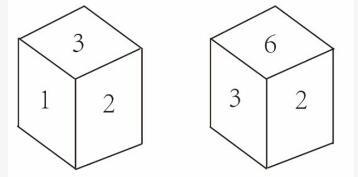
A.1和6
B.2和5
C.3和4
D.4和5

参考解析

解析：第一步，明确提问方式。
从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，选择不可能是相对的两个面。
第二步，找规律。
根据题干可知，两个图中都出现了面2，面2的相邻面分别是1、3、6，根据六面体面之间的关系，可知面4或者面5与面2为相对面，那么面4和面5就不能是彼此的相对面。
因此，选择D选项。

相关考题：

将27个边长为1的小正方体垒成一个大正方体，然后把大正方体全部涂成红色，请问：三面都被涂成红色的小正方体有多少个？（）。A.4B.6C.8D.12
查看答案
有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6。将两个正方体放在桌面上，向上的一面数字之和为偶数的有多少种情形?（ ）A．9B．12C．18D．24
查看答案
将右边的箔片沿虚线折起来，便可做一个正方体。问这个正方体的3号面对面是几号面？( )A.1B.2C.5D.6
查看答案
如图可以折成一个正方体，面l与面____相对;面2与面____相对。
查看答案
题干图形是一个正方体和三棱柱的组合，将其从任一面剖开，下面哪一项不可能是该立体图形的截面？
查看答案
在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A.1/4B.1/6C.1/8D.1/10
查看答案
一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）A. 0.05B. 0.17C. 0.34D. 0.67
查看答案
将右边的箔片沿虚线折起来，便可做一个正方体。问这个正方体的3号面对面是几号面？( ) A. 1B. 2C. 5D. 6
查看答案
边长为6的正方体，由若干个边长为1的正方体组成，现将大正方体表面涂上色，请问仅有一面着色的小正方体与仅有两面着色的小正方体个数之差为多少？A.36B.48C.54D.64
查看答案
如图所示是从两个不同角度观察到的同一个正四面体的外表面，将该四面体展开，可能得到的图形是（）。A.如上图所示B.如上图所示C.如上图所示D.如上图所示
查看答案
有一批边长为1厘米的小正方体，其中一面涂红色的有400个，相邻两面涂红色的有30个，相邻三面涂红色的有1个，其余小正方体各面都没有涂颜色。用这一批小正方体组成一个大正方体，要求这个大正方体有三个面是红色，且这三个面两两相邻，其余的三个面没有颜色。假如没有涂颜色的小正方体数量足够多，那么这个正方体的边长最大是（ ）厘米。A.10B.11C.12D.13
查看答案
将棱长为1的正方体的六个面的中点相连接可以得到一个八面体，则这个八面体的体积为：
查看答案
连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，问正八面
查看答案
连接正方体每个面的中心构成一个正八面体（如下图所示）。已知正方体的边长为6厘 米，问正八面体的体积为多少立方厘米？（ ）
查看答案
边长为4的正方体木块，各面均涂成红色，将其锯成64个边长为1的小正方体，并将它们搅匀混在一起，随机抽取一个小正方体，恰有两面为红色的概率是（ ）
查看答案
在下列正立方体六个表面上挖出三个由小正方体拼成的洞如下图所示，已知三个洞均完全连通两个相对的面，则挖出部分的形状是：A.如上图所示B.如上图所示C.如上图所示D.如上图所示
查看答案
下图是由六个棱长为1的正方体组成的几何体，其主视图的面积是( )。 A.3B.4C.5D.6
查看答案
（）是由六个正方形的面构成6A、正方体B、圆柱体C、三角体D、圆锥体
查看答案
正方体上的六个面各作用有一个平面汇交力系，则该力系独立的平衡方程最多有（）A、4个；B、6个；C、8个；D、12个
查看答案
单选题在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A 1/4B 1/6C 1/8D 1/10
查看答案
热门标签