设,则I,J,K的大小关系为 A.AIB.IC.JD.K
设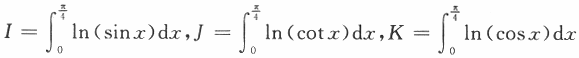 ,则I,J,K的大小关系为
,则I,J,K的大小关系为
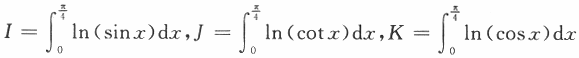 ,则I,J,K的大小关系为
,则I,J,K的大小关系为
A.AI
参考解析
解析:同一区间上定积分大小比较最常用的思想就是比较被积函数大小.由于当 时,0
时,0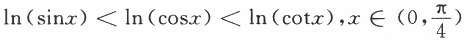
故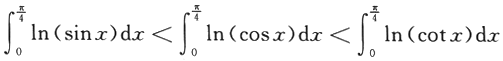 ,即I
,即I
 时,0
时,0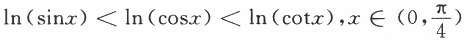
故
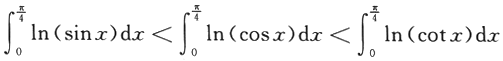 ,即I
,即I相关考题:
已知有一维数组A[0...m*n-1],若要对应为m行、n列的矩阵,则下面的对应关系______可将元素A[k](0≤k<m*n)表示成矩阵的第i行、第j列的元素(0≤i<m,0≤j<n)。A.i=k/n,j=k%mB.i=k/m,j=k%mC.i=k/n,j=k%nD.i=k/m,j=k%n
利用动态规划法求解每对节点之间的最短路径问题时,设有向图G=共有n个节点,节点编号1~n,设C 利用动态规划法求解每对节点之间的最短路径问题时,设有向图G=<V,E>共有n个节点,节点编号1~n,设C是G的成本邻接矩阵,用Dk(i,j)表示从i到j并且不经过编号比k还大的节点的最短路径的长度(Dn(i,j)即为图G中节点i到j的最短路径长度),则求解该问题的递推关系式为(28)。A.Dk(i,j)=Dk-1(i,j)+C(i,j)B.Dk(i,j)=min{Dk-1(i,j),Dk-1(i,j)+C(i,j)}C.Dk(i,j)=Dk-1(i,k)+Dk-1(k,j)D.Dk(i,j)=min{Dk-1(i,j),Dk-1(i,k)+Dk-1(k,j)}
利用动态规划方法求解每对节点之间的最短路径问题(all pairs shortest path problem)时,设有向图 G=<V,E>共有n个节点,节点编号1~n,设C是G的成本邻接矩阵,用Dk(I,j)即为图G中节点i到j并且不经过编号比k还大的节点的最短路径的长度(Dn(i,j)即为图G中节点i到j的最短路径长度),则求解该问题的递推关系式为(62)。A.Dk(I,j)=Dk-1(I,j)+C(I,j)B.Dk(I,j)=Dk-1(I,k)+Dk-1(k,j)C.Dk(I,j)=min{Dk-1(I,j),Dk-1(I,j)+C(I,j)}D.Dk(I,j)=min{Dk-1(I,j),Dk-1(I,K)+Dk-1(k,j)}
设关系模式R,其中U{H,I,J,K,L},若F={H→IJ,J→K,IJK→L,L→H,L→K),则F的最小函数依赖集Fmin={(5 设关系模式R<U,F>,其中U{H,I,J,K,L},若F={H→IJ,J→K,IJK→L,L→H,L→K),则F的最小函数依赖集Fmin={(54)},关系模式R的候选关键字是(55)。A.H→I,H→J,J→K,IJK→L,L→HB.H→I,H→J,J→K,IJ→L,L→HC.H→I,H→J,J→K,IJ→L,J→KD.H→I,J→K,IJ→L,L→H,L→K
已知有一维数组A(0..m*n-1],若要对应为m行、n列的矩阵,则下面的对应关系(4)可将元素A[k](0≤k<m*n)表示成矩阵的第i行、第j列的元素(0≤i<m,0≤j<n)。A.i=k/n,j=k%mB.i=k/m,j=K%mC.i=k/n,j=k%nD.i=k/m,j=k%n
设关系模式Rm,其中U={H,I,J,K,L},若F={H→IJ,J→K,IJK→L,L→H,L→K},则F 的最小函数依赖集Fmin= 设关系模式Rm<U,F>,其中U={H,I,J,K,L},若F={H→IJ,J→K,IJK→L,L→H,L→K},则F 的最小函数依赖集Fmin={(35)}。关系模式R 的候选关键字有(36)个,R 属于(37)。A.H→I,H→J,J→K,IJK→L,L→HB.H→I,H→J,J→K,IJ→L,L→HC.H→I,H→J,J→K,IJ→L,L→KD.H→I,J→K IJ→L,L→H,L→K
设直线的方程为则直线:(A)过点(1,-1,0),方向向量为2i + j-k(B)过点(1,-1,0),方向向量为2i - j + k(C)过点(-1,1,0),方向向量为-2i - j + k(D)过点(-1,1,0),方向向量为2i + j - k
已知有一维数组A[0.m×n-1],若要对应为m行n列的矩阵,则下面的对应关系(),可将元素A[k](O≤<k≤<m×n)表示成矩阵的第i行、第j列的元素(0≤i≤m,0匀≤n)。 A. i=k/n,j=k%mB.i=k/m,j=k%mC.i=k/n,j=k%nD.i=k/m,j=k%n
设某n阶三对角矩阵Anxn的示意图如下图所示。若将该三对角矩阵的非零元素按行存储在一维数组B[k](1≤k≤3*n-2)中,则k与i、j的对应关系是( )。A.k=2i+j-2B.k=2i-j+2C.k=3i+j-1D.K=3i-j+2
单选题设向量a=2i+j-k,b=i-j+2k,则a×b为().Ai+5j+3kBi-5j+3kC5j-3kD1+5j-3k