将一根绳子任意分成三段,则此三段能构成一个三角形的概率是:
将一根绳子任意分成三段,则此三段能构成一个三角形的概率是:


参考解析
解析:第一步,本题考查概率问题,需结合几何性质解题。
第二步,设线段长度为a,任意分成三段长分别为x,y和a-x-y,显然有x>0,y>0,a-x-y>0,将这三个约束条件画到(x,y)二维平面坐标系上,这三条直线围成了一个直角三角形即为可行域,其面积为1/2a2。
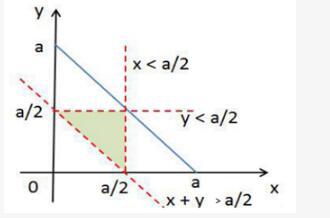

第二步,设线段长度为a,任意分成三段长分别为x,y和a-x-y,显然有x>0,y>0,a-x-y>0,将这三个约束条件画到(x,y)二维平面坐标系上,这三条直线围成了一个直角三角形即为可行域,其面积为1/2a2。


相关考题:
有人测量一座桥离水面的高度,将一根绳子对折,碰到水面时绳子还剩下 6 米(按对折 后的长度算);把绳子平均折成三段,碰到水面时绳子还剩下 2 米。 问桥高多少米A.2 B.4 C.6 D.8
你一番判断之后,终于找到了应该受奖励的小徒弟。这时老者拿起书案上的一根细绳,先把绳子对折三次,然后把对折后的绳子剪成了三段。笑眯眯的看着你说:“请问智者,现在我这有多少段绳子?”你应该如何回答老者呢?现在老者那里一共有__________段绳子。
填空题已知一个有效三段论的小前提是O命题,则此三段论是第()格()式。