从100个住户中随机抽取了10户,调查其月消费支出额。经计算得到10户的平均月消费支出额为3500元,标准差为300元。假定总体服从正态分布,则总体平均月消费支
从100个住户中随机抽取了10户,调查其月消费支出额。经计算得到10户的平均月消费支出额为3500元,标准差为300元。假定总体服从正态分布,则总体平均月消费支
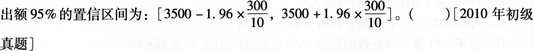
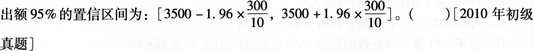
参考解析
解析:

相关考题:
:下列说法不正确的是( )。A.该市城镇居民的人均消费收入高于农民B.城镇居民的人均消费性支出额均高于同期农民人均消费性支出额C.1999年~2004年农民人均消费性支出增长幅度总体上低于城镇居民人均消费性支出增长幅度D.相对于城镇居民,该市农民的人均消费支出金额增长量小
某地区居民户数为10000户,其平均月消费水平标准差为100元。采取简单随机重复抽样抽取样本进行调查,以了解其月平均消费水平,若可靠程为95.45%,误差不超过10元,则应抽取()户居民进行调查。
某地区居民户数为10000户,其平均月消费水平标准差为100元。采取简单随机重复抽样抽取样本进行调查,以了解其月平均消费水平,若可靠程序为95.45%,误差不超过10元,则应抽取()户居民进行调查。 A、100户B、200户C、400户D、1000户
(一)某地区家计调查资料得知,每户平均月收入()为8000元,标准差为800元,每户平均月消费支出()5200元,方差为40000元,收入与支出的协方差(=r××)为157000元,支出对于收入的回归系数为0.2。请根据上述资料回答下列问题: 收入与消费支出的相关系数为( )。A.0.96B.0.95C.0.97D.0.98
在某城市随机抽取1000户居民作为样本对该城市居民消费水平进行研究,对居民月消费支出Y(单位:元)和月收入X(单位:元),建立回归模型,得到估计的回归方程Y=1300+0.6X,决定系数0.96,关于该模型的说法正确的有( )。A.居民月收入和月消费支出之间正相关B.回归模型的拟合效果很好C.居民月收入难以解释月消费支出的变化D.居民月收入每增长1元,月消费支出将平均增长0.6元E.居民月收入为10000时,居民人均月消费支出大约为7300元
表3—1是2006年中国31个主要城市年平均相对湿度的数据(单位:%)。31个城市的年平均相对湿度可以视为从全国所有城市中抽取的随机样本。假定全国年平均相对湿度服从正态分布,且总体标准差为11,则全国年平均相对湿度95%置信度的区间估计为( )。
从某企业90名员工中依据工号随机抽取10名员工调查其6月份的医疗费支出。相关调查结果如表1所示:请根据上述资料回答下列问题:假设总体服从正态分布,全公司员工平均医疗费支出95%的置信区间为()。(备注:样本均值为190,样本标准差为251.53,)A.置信上限为B.置信上限为C.置信下限为D.置信下限为
某大学一家快餐店记录了过去5年每天的营业额,每天营业额的均值为2500元,标准差为400元,由于在某些节日的营业额偏高,所以每日营业额的分布是右偏的。从5年中随机抽取100天,计算其平均营业额,则其抽样分布是()A、正态分布,均值为250元,标准差为40元B、正态分布,均值为2500元,标准差为40元C、右偏,均值为2500元,标准差为400元D、正态分布,均值为2500元,标准差为400元
由64名超市顾客组成的随机样本显示顾客的平均消费金额为43美元。假设该分布符合正态分布,且总体标准差为15美元,则总体平均值的90%的置信区间最接近于()A、41.085~44.915B、40.218~45.782C、39.916~46.084
从麦当劳餐厅连续三个星期抽查49位顾客,以调查顾客的平均消费额,得样本平均消费额为25.5元。要求: (1)假如总体的标准差为10.5元,那么抽样平均误差是多少? (2)在0.95的概率保证下,抽样极限误差是多少?极限误差说明什么问题? (3)总体平均消费额95%的信赖区间是多少?
随机从某地人口总体中,抽得100人构成样本,测得100人的平均身高为168cm。又据经验和以往资料知身高服从正态分布,身高的标准差为4cm,问在1%和5%的显著性水平下,是否可认为人口总体的平均身高为167cm。
某学院共有1000名学生,现欲了解学生的每月生活消费情况,随机抽取50名学生的月生活消费数据对1000名学生的情况进行估算。这50名学生的平均月消费是()。A、总体参数B、总体C、样本D、样本统计量
某城市统计局想知道当地居民每月的平均食物消费水平,假设居民食物消费水平近似服从正态分布,根据经验,他们设定居民每月的平均食物消费水平为500元(原假设),随机抽取了100位当地居民并统计当月食物消费,得出均值为520元,标准差为40元,若显著性水平α=0.05,由此可以判断:()A、居民每月的平均食物消费水平高于500元B、没有足够的理由拒绝“居民每月的平均食物消费水平为500元”的原假设C、样本含量少,不足以做出任何判断D、由于样本均值为520元,标准差为40元,根据正态分布的特点,一定有不少居民食物消费水平低于500元,因此平均食物消费水平也有可能低于500元
某地区居民户数为10000户,其年消费水平标准差为150元。若采取抽样调查了解其年平均消费水平,并以95%的置信度(相对应的函数值为1.96)推断总体,其样本指标与总体指标之间的允许误差范围是20元。要求:用公式计算出应抽查多少居民户?
单选题在一个学校里随机抽取50名学生调查午餐的消费额。现得到在90%的置信度下学生午餐的平均消费区间是(3.45元,4.15元).下面哪种说法是正确的()A这个学校90%的学生午餐消费额在(3.45元,4.15元)B这个学校90%的学生午餐平均消费额在(3.45元,4.15元)C随机样本的90%学生午餐消费额在(3.45元,4.15元)D样本量为50的所有可能样本中的90%学生午餐平均消费额在(3.45元,4.15元)
问答题某地区居民户数为10000户,其年消费水平标准差为150元。若采取抽样调查了解其年平均消费水平,并以95%的置信度(相对应的函数值为1.96)推断总体,其样本指标与总体指标之间的允许误差范围是20元。要求:用公式计算出应抽查多少居民户?
单选题某大学一家快餐店记录了过去5年每天的营业额,每天营业额的均值为2500元,标准差为400元,由于在某些节日的营业额偏高,所以每日营业额的分布是右偏的。从5年中随机抽取100天,计算其平均营业额,则其抽样分布是()A正态分布,均值为250元,标准差为40元B正态分布,均值为2500元,标准差为40元C右偏,均值为2500元,标准差为400元D正态分布,均值为2500元,标准差为400元