假设某商品需求函数为Q=100-2P,供给函数为Q=20+6P。 (1)该商品的市场均衡价格和销售量是多少? (2)如果政府对该商品征收每单位商品4元的数量税,市场均衡的销售量是多少?消费者支付的价格和生产商接受的价格分别是多少?税收负担如何分配? (3)如果商品供给函数变为Q= 40+6P,题目(1)和(2)中的答案该如何变化?
假设某商品需求函数为Q=100-2P,供给函数为Q=20+6P。 (1)该商品的市场均衡价格和销售量是多少? (2)如果政府对该商品征收每单位商品4元的数量税,市场均衡的销售量是多少?消费者支付的价格和生产商接受的价格分别是多少?税收负担如何分配? (3)如果商品供给函数变为Q= 40+6P,题目(1)和(2)中的答案该如何变化?
参考解析
解析:(1)联立需求函数和供给函数可得:100-2P=20+6P解得:均衡价格P=10。将P=10代入需求函数或供给函数可得销售量为80。 (2)如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足
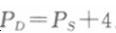
联立以下四个方程:
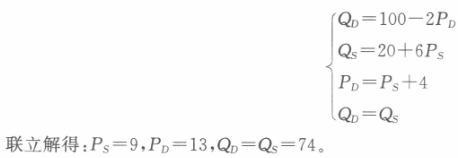
即市场均衡的销售量为74,消费者支付的价格为每单位13元,生产商接受的价格为每单位9元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 (3)联立需求函数和供给函数可得:100-2P=40+6P解得:均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足PD—PS+4。联立以下四个方程:
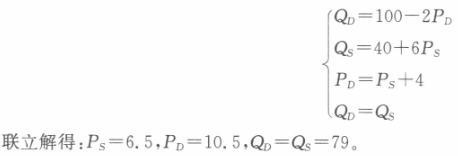
即市场均衡的销售量为79,消费者支付的价格为每单位10.5元,生产商接受的价格为每单位6.5元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 可以看出,由于供给曲线斜率不变,所以税负的转嫁程度不变,因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。
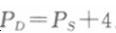
联立以下四个方程:
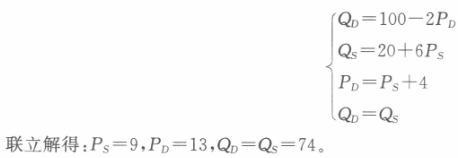
即市场均衡的销售量为74,消费者支付的价格为每单位13元,生产商接受的价格为每单位9元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 (3)联立需求函数和供给函数可得:100-2P=40+6P解得:均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足PD—PS+4。联立以下四个方程:
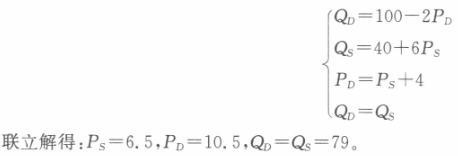
即市场均衡的销售量为79,消费者支付的价格为每单位10.5元,生产商接受的价格为每单位6.5元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 可以看出,由于供给曲线斜率不变,所以税负的转嫁程度不变,因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。
相关考题:
已知某商品的需求函数和供给函数分别为:Qd=34—6P,Qs=6+8P,该商品的 均衡价格是( )A.5/3 已知某商品的需求函数和供给函数分别为:Qd=34—6P,Qs=6+8P,该商品的 均衡价格是( )A.5/3B.5/4C.5/2D.2
假定某完全竞争行业有100个相同的厂商,单个厂商的短期总成本函数为.STC=Q2+6Q +20。 (l)求市场的短期供给函数。 (2)假定市场的需求函数为Qd=420 - 30P,求该市场的短期均衡价格和均衡产量。 (3)假定政府对每一单位商品征收1.6元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?消费者和厂商各自负担多少税收?
假定某完全竞争市场的需求函数为Qd= 68 -4P,行业的短期供给函数为Qs= -12 +4P: (1)求该市场的短期均衡价格和均衡产量。 (2)在(1)的条件下,该市场的消费者剩余、生产者剩余和社会总福利分别是多少? (3)假定政府对每一单位商品征收2元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?此外,消费者剩余、生产者剩余和社会总福利的变化又分别是多少?
某垄断企业的总成本函数为市场需求曲线为(2)假设政府对该垄断企业征收每单位商品1元的单位税(数量税),该垄断商品的市场价格、企业的产量和利润分别为多少?政府获得的税收收入为多少? (3)假设政府不对垄断企业,而对消费者征收每单位商品1元的单位税,该垄断市场的商品价格、企业的产量和利润分别为多少?政府获得的税收收入是多少?
假设某完全竞争行业有500个相同的厂商,每个厂商的短期成本函数为:STC=O. 5Q2+Q+10。 (1)求完全竞争市场的短期供给函数。 (2)假设市场需求函数为QD=4 000-400P,求市场的均衡价格和产量。 (3)假定对每一件产品征收0.9元的税,新的市场均衡价格和产量又为多少?厂商和消费者的税收负担各为多少?
已知某一时期内某商品的需求函数为Q’=50-5P,供给函数为Q=-10+5P (1)求均衡价格Pe和均衡数量Qe,并作出几何图形。 (2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd= 60 -5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs= -5 +5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (4)利用(1)、(2)和(3).说明静态分析和比较静态分析的联系和区别。 (5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格与均衡数量的影响。
已知某一时期内某商品的需求量为300万件,市场供给量是200万件。价格每波动1元,会引起销量变动2万件。<1> 、求该商品的均衡价格和均衡数量。<2> 、如果市场对该商品需求进一步扩大,则可能引起的情形有哪些 <3> 、假设商品供给量达到220万件,求该商品的均衡价格。<4> 、如果当前商品市场价格是18元/件,则可能引起的情形有哪些
已知某一时期内某商品的需求函数Qd=300-10P,供给函数为Qs=100+10P。 、计算该商品的均衡价格和均衡数量。 、分别计算下列不同情况下的均衡价格和均衡数量。①假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=500-10P。②假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=200+10P。 、根据供求定理,当供给不变时,需求量的增加或减少会引起需求曲线、均衡价格和均衡数量怎样的变动?当需求不变时,供给量的增加或减少又将引起供给曲线、均衡价格和均衡数量怎样的变动?
某企业商品的需求价格函数为P=100-4Q,供给价格函数为P=40+2Q,则该商品的均衡价格和均衡产量分别为()。A:P=10,Q=6B:P=60,Q=10C:P=40,Q=6D:P=20,Q=
某一时期内A商品的需求函数为Qd=50-5P,供给函数为Qs=10+5P。其中,Qd为需求量,Qs为供给量,P为价格。A商品的均衡价格与均衡数量分别为()。A.P=5,q=20B.P=4,Q=30C.P=5,q=15D.P=6,Q=15
已知某一时期内某商品的需求函数为Qd=50-5P,供给函数为Qs=-10+5P。假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。求出相应的均衡价格Pε和均衡产量Qε。
计算题: 已知某商品在某市场特定时期的需求函数是:QD、=14—3P,供给函数为:QS=2+6P试求: (1)该商品的均衡价格和均衡数量。 (2)均衡时的需求价格弹性。 (3)该产品适合降价吗?为什么?
某企业商品的需求价格函数为P=100-4Q,供给价格函数为P=40+2Q,则该商品的均衡价格和均衡产品分别为( )。A、P=10Q=6B、P=60Q=10C、P=40Q=6D、P=20Q=20
单选题某企业商品的需求价格函数为P=100-4Q 供给价格函数为P=40+2Q 则该商品的均衡价格和均衡产量分别为()AP=10 Q=6BP=60 Q=10CP=40 Q=6DP=20 Q=20
问答题假设市场中有大量企业,每家企业的长期生产函数都相同,为LC=Q3-4Q2+8Q。 (1)试求该市场达到长期均衡的价格; (2)如果市场需求函数为Q=2000-1OOP,在市场达到长期均衡时,市场交易量是多少?市场中容纳了多少家企业?
问答题考虑某消费者购买商品A的替代效应与收入效应。假定该消费者关于商品A的需求函数为Q=0.02M-2P,收入M=6500,商品A的价格P=20。如果目前商品A的价格上升为P=40。求:商品A的价格变化的总效应是多少?其中替代效应与收入效应又分别是多少?