均质圆环的质量为半径为圆环绕O轴的摆动规律为φ=ωt,ω为常数。图 4-74所示瞬时圆环对转轴O的动量矩为( )。A. mR2ω B. 2mR2ω C. 3mR2ω D. 1/2mR2ω
均质圆环的质量为半径为圆环绕O轴的摆动规律为φ=ωt,ω为常数。图 4-74所示瞬时圆环对转轴O的动量矩为( )。
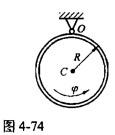
A. mR2ω B. 2mR2ω C. 3mR2ω D. 1/2mR2ω

A. mR2ω B. 2mR2ω C. 3mR2ω D. 1/2mR2ω
参考解析
解析:提示:定轴转动刚体的动量矩为:LO=JOω。
相关考题:
质量为m,半径为R的均质圆轮,绕垂直于图面的水平轴O转动,其角速度为w。在图示瞬时,角加速度为0,轮心C在其最低位置,此时将圆轮的惯性力系向O点简化, 其惯性力主矢和惯性力主矩的大小分别为:
如图所示,曲柄OA长R,以匀角速度ω绕O轴转动,均质圆轮B在水平面上做纯滚动,其质量为m,半径为r。在图示瞬时,OA杆铅直。圆轮B对接触点C的动量矩为( )mRrω。A.0.5B.1.0C.1.5D.2.0
如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。
单选题均质圆环的质量为m,半径为R,圆环绕O轴的摆动规律为φ=ωt,ω为常数。图4-74所示瞬时圆环对转轴O的动量矩为()。AmR2ωB2mR2ωC3mR2ω