f(x)在点x0处的左、右极限存在且相等是f(x)在点x0处连续的( )。A、 必要非充分的条件B、 充分非必要的条件C、 充分且必要的条件D、 既非充分又非必要的条件
f(x)在点x0处的左、右极限存在且相等是f(x)在点x0处连续的( )。
A、 必要非充分的条件
B、 充分非必要的条件
C、 充分且必要的条件
D、 既非充分又非必要的条件
B、 充分非必要的条件
C、 充分且必要的条件
D、 既非充分又非必要的条件
参考解析
解析:函数f(x)在点x0处连续的充要条件为:在该点处的左右极限存在且相等,并等于函数在该点处的函数值,即:
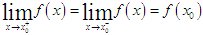
故f(x)在点x0处的左、右极限存在且相等,并不能得出f(x)在点x0处连续,也可能是可去间断点,为必要非充分条件。
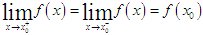
故f(x)在点x0处的左、右极限存在且相等,并不能得出f(x)在点x0处连续,也可能是可去间断点,为必要非充分条件。
相关考题:
以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0D.若函数f(x)在点x0处连续,则f'(x0)一定存在
下列结论不正确的是()。A、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处连续B、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处可导C、z=f(x,y)在点(x0,y0)处可导,则f(x,y)在点(x0,y0)处可微D、z=f(x,y)在点(x0,y0)处偏导数连续,则f(x,y)在点(x0,y0)处连续
设g(x)在(-∞,+∞)严格单调递减,且f(x)在x=x0处有极大值,则必有()。A、g[f(x)]在x=x0处有极大值B、g[f(x)]在x=x0处有极小值C、g[f(x)]在x=x0处有最小值D、g[f(x)]在x=x0既无极值也无最小值
下列结论不正确的是()。A、y=f(x)在点x0处可微,则f(x)在点x0处连续B、y=f(x)在点x0处可微,则f(x)在点x0处可导C、y=f(x)在点x0处连续,则f(x)在点x0处可微D、y=f(x)在点x0处可导,则f(x)在点x0处连续
单选题以下关于二元函数的连续性的说法正确是( )。A若f(x,y)沿任意直线y=kx在点x=0处连续,则f(x,y)在(0,0)点连续B若f(x,y)在点(x0,y0)点连续,则f(x0,y)在y0点连续,f(x,y0)在x0点连续C若f(x,y)在点(x0,y0)点处偏导数fx′(x0,y0)及fy′(x0,y0)存在,则f(x,y)在(x0,y0)处连续D以上说法都不对
单选题设f(x)g(x)在x0处可导,且f(x0)=g(x0)=0,f′(x0)g′(x0)>0,f″(x0)、g″(x0)存在,则( )Ax0不是f(x)g(x)的驻点Bx0是f(x)g(x)的驻点,但不是它的极值点Cx0是f(x)g(x)的驻点,且是它的极小值点Dx0是f(x)g(x)的驻点,且是它的极大值点
单选题考虑二元函数f(x,y)的下面4条性质:①f(x,y)在点(x0,y0)处连续;②f(x,y)在点(x0,y0)处的两个偏导数连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q,则有( )。A②⇒③⇒①B③⇒②⇒①C③⇒④⇒①D③⇒①⇒④
单选题设y=f(x)满足关系式y″-2y′+4y=0,且f(x0)>0,f′(x0)=0,则f(x)在x0点处( )。A取得极大值B取得极小值C在x0点某邻域内单调增加D在x0点某邻域内单调减少
单选题设f′(x0)=f″(x0)=0,f‴(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( )。Af′(x0)是f′(x)的极大值Bf(x0)是f(x)的极大值Cf(x0)是f(x)的极小值D(x0,f(x0))是曲线y=f(x)的拐点
单选题下列说法中正确的是( )。[2014年真题]A若f′(x0)=0,则f(x0)必须是f(x)的极值B若f(x0)是f(x)的极值,则f(x)在点x0处可导,且f′(x0)=0C若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的必要条件D若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的充分条件
单选题如果函数f(x)当x→x0时极限存在,则函数f(x)在点x0处( )。A有定义B无定义C不一定有定义D连续