一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率υ=550Hz，波速u=330m·s-1。若t=0时，坐标原点O处质元达到负的最大位移，则该波的表达式为( )。A、y=0.01cos[2π(550t+1.67x)+π]B、y=0.01cos[2π(550t-1.67x)+π]C、y=0.01cos[2π(550t+1.67x)-π]D、y=0.01cos[2π(550t-1.67x)-π]

一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率υ=550Hz，波速u=330m·s-1。若t=0时，坐标原点O处质元达到负的最大位移，则该波的表达式为( )。

A、y=0.01cos[2π(550t+1.67x)+π]
B、y=0.01cos[2π(550t-1.67x)+π]
C、y=0.01cos[2π(550t+1.67x)-π]
D、y=0.01cos[2π(550t-1.67x)-π]

参考解析

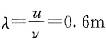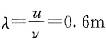解析：按题设A=0.01m，v=550Hz，u=330m·s-1则波长按题意，原点处质元达到负的最大位移，即y0=-A，v0=0，初相φ0=π，则O点处质元的振动方程为y0=Acos(ωt+φ0)=0.01cos[2π(550t)+1π]，因为波沿x轴负方向传

相关考题：

一平面简谐波在t=0时的波形曲线如图所示，设波沿x轴正向传播，波速υ=1.6×10-1m/s，则该波的角频率ω=______rad/s，坐标原点处的质元作简谐振动的表达式为y=_____(SI)。
查看答案
一简谐波沿x轴正向传播，波的振幅为A，角频率为ω，波速为u。若以原点处的质元经平衡位置正方向运动时作为计时的起点，则该波的波动方程是( )。A.y=Acos[ω(t-x/u)+π/2]B.y=Acos[ω(t-x/u)-π/2]C.y=Acos[ω(t-x/u)+π]D.y=Acos[ω(t-x/u)-π/3]
查看答案
—平面简谐波沿x轴正方向传播，振幅A=0. 02m，周期T=0. 5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为：A.y=0.02cos2π(t/2-0.01x) (SI)B.y=0.02cos2π(2t-0.01x) (SI)C.y=0.02cos2π(t/2-100x) (SI)D.y=0.02cos2π(2t-100x) (SI)
查看答案
一振幅为A，周期为T，波长λ的平面简谐波沿x轴负向传播，在x=λ/2处，t=T/4时，振动相位为π，则此平面简谐波的波动方程为( )。A.B.C.D.
查看答案
已知一列平面简谐波沿Ox轴正向传播，波速u=400m·s-1，频率υ=20Hz，t=0时刻的波形曲线如图3所示，则波动表达式为( )。
查看答案
一平面简谐波表达式为y=-0.05sinπ(t-2x)(SI)，则该波的频率v(Hz)、波速u(m/s)及波线上各点振动的振幅A(m)依次为：
查看答案
一平面余弦波波源的振动周期T=0.5s，所激起的波的波长λ=10m，振幅为0.5m，当t=0时，波源处振动的位移恰为正向最大值，取波源处为原点并设波沿x轴正向传播，此波的波动方程为( )。
查看答案
一平面谐波沿x轴正方向传播，振幅A=0.02m，周期T=0.5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为( )。A.B.y=0.02cos2π(2t-0.01x)(SI)C.D.y=0.02cos2π(2t-100x)(SI)
查看答案
—平面简谐波沿x 轴正方向传播 ，振幅A=0.02m ，周期T=0.5s ，波长λ= 100m ，原点处质元的初相位Φ=0，则波动方程的表达式为：
查看答案
一质点沿y轴方向做简谐振动，振幅为A，周期为T，平衡位置在坐标原点。在t=0时刻，质点位于y正向最大位移处，以此振动质点为波源，传播的横波波长为λ，则沿x轴正方向传播的横波方程为（ ）。
查看答案
一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率v=550Hz，波速u=330m/s。若t=0时，坐标原点处的质点达到负的最大位移，则此波的波函数为（ ）。
查看答案
一平面简谐波沿x轴正向传播，已知x=L（Lλ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）A、y=Acosω［t-（x-L）／u]B、y=Acosω［t-（x+L）／u]C、y=Acosω［t+（x+L）／u]D、y=Acosω［t+（x-L）／u]
查看答案
一列横波沿x轴正方向传播，它的波动表达式为y=0.02cosπ（5x-200t），则下列说明正确的是（）。 （1）其振幅为0.02m； （2）频率为100Hz； （3）波速为40m·s-1； （4）波沿x轴负向传播。A、（1）、（2）、（3）、（4）B、（1）、（2）、（3）C、（2）、（3）、（4）D、（1）、（2）、（4）
查看答案
一平面简谐波的表达式为y=Acosω（t-x/u）=Acos（ωt-ωx/u），其中x/u表示波从坐标原点传至x处所需时间。
查看答案
一平面简谐波沿着x轴正方向传播，已知其波函数为y=0.4cosπ(50t-0.10x)m，则该波的振幅为（），波速为（）。
查看答案
一平面简谐波沿X轴正向传播，已知x=L（Lλ）处质点的振动方程为y=Acosωt，波速为u，那么x=0处质点的振动方程为（）。A、y=Acosω（t+L/u）B、y=Acosω（t-L/u）C、y=Acos（ωt+L/u）D、y=Acos（ωt-L/u）
查看答案
若一平面简谐波的表达式为y=0.03cos6π（t+0.01x）（SI），则下面结果中正确的是（）。A、振幅为3mB、周期为1／3sC、波速为10m/sD、传播方向为x轴正向
查看答案
一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率v=550Hz，波速u=330m·s-1。若t=0时，坐标原点O处质元达到负的最大位移，则该波的表达式为（）。A、y=0.01cos[2π（550t+1.67x）+π]B、y=0.01cos[2π（550t-1.67x）+π]C、y=0.01cos[2π（550t+1.67x）-π]D、y=0.01cos[2π（550t-1.67x）-π]
查看答案
机械波的表达式为y=0.03cos6p（t+0.01x）（SI），则（）A、其振幅为3m。B、其周期为（1/3）s。C、其波速为10m/s。D、波沿x轴正向传播。
查看答案
单选题一平面简谐波沿X轴正向传播，已知x=L（Lt，波速为u，那么x=0处质点的振动方程为（）。Ay=Acosω（t+L/u）By=Acosω（t-L/u）Cy=Acos（ωt+L/u）Dy=Acos（ωt-L/u）
查看答案
单选题若一平面简谐波的表达式为y=0.03cos6π（t+0.01x）（SI），则下面结果中正确的是（）。A振幅为3mB周期为1／3sC波速为10m/sD传播方向为x轴正向
查看答案
单选题平面波表达式为y＝0.03cos6π（t+0.01x）（SI）则（）。A其振幅为3mB其周期为1/3sC其波速为10m／sD波沿x正向传播
查看答案
单选题一平面简谐波沿x轴正向传播，已知x=L（Lλ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）Ay=Acosω［t-（x-L）／u]By=Acosω［t-（x+L）／u]Cy=Acosω［t+（x+L）／u]Dy=Acosω［t+（x-L）／u]
查看答案
热门标签