一平面谐波沿x轴正方向传播,振幅A=0.02m,周期T=0.5s,波长λ=100m,原点处质元的初相位φ=0,则波动方程的表达式为( )。A.B.y=0.02cos2π(2t-0.01x)(SI)C.D.y=0.02cos2π(2t-100x)(SI)
一平面谐波沿x轴正方向传播,振幅A=0.02m,周期T=0.5s,波长λ=100m,原点处质元的初相位φ=0,则波动方程的表达式为( )。
A.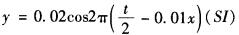
B.y=0.02cos2π(2t-0.01x)(SI)
C.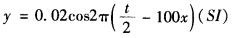
D.y=0.02cos2π(2t-100x)(SI)
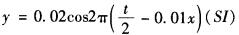
B.y=0.02cos2π(2t-0.01x)(SI)
C.
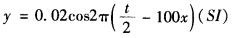
D.y=0.02cos2π(2t-100x)(SI)
参考解析
解析:
相关考题:
一平面简谐波在t=0时的波形曲线如图所示,设波沿x轴正向传播,波速υ=1.6×10-1m/s,则该波的角频率ω=______rad/s,坐标原点处的质元作简谐振动的表达式为y=_____(SI)。
一简谐波沿x轴正向传播,波的振幅为A,角频率为ω,波速为u。若以原点处的质元经平衡位置正方向运动时作为计时的起点,则该波的波动方程是( )。A.y=Acos[ω(t-x/u)+π/2]B.y=Acos[ω(t-x/u)-π/2]C.y=Acos[ω(t-x/u)+π]D.y=Acos[ω(t-x/u)-π/3]
—平面简谐波沿x轴正方向传播,振幅A=0. 02m,周期T=0. 5s,波长λ=100m,原点处质元的初相位φ=0,则波动方程的表达式为:A.y=0.02cos2π(t/2-0.01x) (SI)B.y=0.02cos2π(2t-0.01x) (SI)C.y=0.02cos2π(t/2-100x) (SI)D.y=0.02cos2π(2t-100x) (SI)
一振幅为A、周期为T、波长为λ平面简谐波沿X负向传播,在X=(1/2)λ处,t=T/4时振动相位为π,则此平面简谐波的波动方程为:()A、y=Acos(2πt/T-2πx/λ-1/2π)B、y=Acos(2πt/T+2πx/λ+1/2π)C、y=Acos(2πt/T+2πx/λ-1/2π)D、y=Acos(2πt/T-2πx/λ+1/2π)
一平面简谐波沿x轴正向传播,已知波长λ,频率υ,角频率ω,周期T,初相Ф0,则下列表示波动方程的式子中,哪几个是正确的?Ⅰ.y=Acos(ωt-2πX/λ+Ф0)Ⅱ.y=Acos[2π(t/T-X/λ)+Ф0]Ⅲ.y=Acos[2π(γt-X/λ)+Ф0]()A、ⅠB、Ⅰ、ⅡC、Ⅱ、ⅢD、Ⅰ、Ⅱ、Ⅲ
一平面简谐波沿x轴负方向传播,其振幅A=0.01m,频率v=550Hz,波速u=330m·s-1。若t=0时,坐标原点O处质元达到负的最大位移,则该波的表达式为()。A、y=0.01cos[2π(550t+1.67x)+π]B、y=0.01cos[2π(550t-1.67x)+π]C、y=0.01cos[2π(550t+1.67x)-π]D、y=0.01cos[2π(550t-1.67x)-π]
处于原点(x=0)的一波源所发出的平面简谐波的波动方程为y=Acos(Bt-Cx),其中A、B、C皆为常数。此波的速度为();波的周期为();波长为();离波源距离为l处的质元振动相位比波源落后();此质元的初相位为()。
单选题一平面简谐波沿x轴正向传播,已知波长λ,频率υ,角频率ω,周期T,初相Ф0,则下列表示波动方程的式子中,哪几个是正确的?Ⅰ.y=Acos(ωt-2πX/λ+Ф0)Ⅱ.y=Acos[2π(t/T-X/λ)+Ф0]Ⅲ.y=Acos[2π(γt-X/λ)+Ф0]()AⅠBⅠ、ⅡCⅡ、ⅢDⅠ、Ⅱ、Ⅲ
单选题一振幅为A、周期为T、波长为λ平面简谐波沿X负向传播,在X=(1/2)λ处,t=T/4时振动相位为π,则此平面简谐波的波动方程为:()Ay=Acos(2πt/T-2πx/λ-1/2π)By=Acos(2πt/T+2πx/λ+1/2π)Cy=Acos(2πt/T+2πx/λ-1/2π)Dy=Acos(2πt/T-2πx/λ+1/2π)
单选题一平面简谐波沿x轴正向传播,振幅A=0.02m,周期T=0.5s,波长λ=100m,原点处质元初相位φ=0,则波动方程的表达式( )。[2012年真题]Ay=0.02cos2π(t/2-0.01x)(SI)By=0.02cos2π(2t-0.01x)(SI)Cy=0.02cos2π(t/2-100x)(SI)Dy=0.002cos2π(2t-100x)(SI)