图示质量为m,半径为r的定滑轮O上绕有细绳,依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为a,0
图示质量为m,半径为r的定滑轮O上绕有细绳,依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为a,0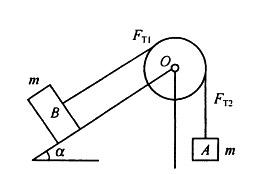



参考解析
解析:在右侧物重力作用下,滑轮顺时针方向转动,故轮上作用的合力矩应有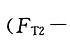

答案:B
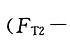

答案:B
相关考题:
图示在倾角为α的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为:A. (k/m)1/2B.[k/(ms)]1/2C. [k/(msinα)]1/2D. (ksinα/m)1/2
一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
图示两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r,并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m,对轴O的回转半径为ρ0外。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
图示质量为m,半径为r的定滑轮O上绕有细绳,依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾斜角为α,0T1和FT2的大小有关系:A. FT1= FT2 B.FT1T2 C. FT1>FT2 D.只依据已知条件则不能确定
圆轮上绕一细绳,绳端悬挂物块,物块的速度为v、加速度a,圆轮与物块的直线段相切之点为P,该点速度与加速度的大小分别为:(A)vp=v,ap>a(B)vp>v,ap<a(C)vp=v,ap<a(D)vp>v,ap>a
两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为ρO。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
圆轮上绕一细绳,绳端悬挂物块。物块的速度v、加速度a。圆轮与绳的直线段相切之点为P,该点速度与加速度的大小分别为:A. vp = v,ap>a B. vp>v,apC. vp =v,app>v,ap>a
质量为m,半径为r 的定滑轮O 上绕有细绳。依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m 的物块A 与B。块B放置的光滑斜面倾角为α ,假定定滑轮O 的轴承光滑,当系统在两物块的重力作用下开始运动时,B与O间,A 与O间的绳力FT1和FT2的大小有关系:(A) FT1=FT2(B) FT1 T2(C) FT1 >FT2(D)只根据已知条件不能确定
两重物的质量均为m,分别系在两软绳上,此两绳又分别绕在半径各为r与2r并固结一起的两圆轮上,两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为p0,两重物中一铅垂悬挂,一置于光滑平面上,当系统在左重物重力作用下运动时,鼓轮的角加速度a为:
图示鼓轮半径r=3.65m,对转轴O的转动惯量JO= 0.92kg ? m2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:A. 37.8N ? m B. 47N ? mC. 36.3N ? m D. 45.5N ? m
如图8-2所示,物块A放在水平的光滑桌面上,用细绳的一端系住A绳穿过小孔O,另一端系物块B.当A在桌面上以角速度ω=5 rad/s绕O做匀速圆周运动时,绳被拉紧,B静止才动.已知A的质量mA=1 kg,A离O的距离为1 m,则B的质量等于( )(取g=10 m/s2)A.2.5 kgB.2 kgC.1.5 kgD.0.5 kg
如图所示的装置中,物块A、B、C的质量分别为M、m和mo,物块曰放置在物块A上,物块A用不可伸长的轻绳通过滑轮与物块C连接,绳与滑轮之间的摩擦不计。若日随A一起沿水平桌面做匀速运动,则可以断定(重力加速度为9)( )。 A.物块A与桌面之间有摩擦力,大小为,mog B.物块A与B之间有摩擦力.大小为mog C.桌面与A之间,B与A之间,都有摩擦力,两者方向相同,它们的合力为mog D.桌面与A之间,B与A之间,都有摩擦力,两者方向相反,它们的合力为meg
确定物体绕某个轴的转动惯量,可以由理论计算也可通过实验测定。(1)用积分计算质量为m,半径为R的均质薄圆盘绕其中心轴的转动惯量。(2)该圆盘质量未知,可用如图9所示的实验方法测得该圆盘绕中心轴的转动惯量。在圆盘的边缘绕有质量不计的细绳,绳的下端挂一质量为m的重物,圆盘与转轴间的摩擦忽略不计。测得重物下落的加速度为a,求圆盘绕其中心轴的转动惯量。
圆柱体定滑轮的质量为m,半径为R,绕其质心轴转动的角位移为θ=a+bt+ct2,a、b、c为常数,作用在定滑轮上的力矩为()A、(1/2)maR2B、bmR2C、(1/2)mbR2D、mcR2
单选题图示鼓轮半径r=3.65m,对转轴O的转动惯量Jo=0.92kg·m 2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:()A 37.8N.mB 47N.mC 36.3N.mD 45.5N.m
单选题质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC= 。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。A K=0B K=mRwC K=mRwD K=2mRw