半径R=10cm的鼓轮,由挂在其上的重物带动而绕O轴转动,如图所示。重物的运动方程为x= 100t2(x以m计,t以s计)。则鼓轮的角加速度α的大小和方向是:A.α=2000rad/s2,顺时针向B. α==2000rad/s2,逆时针向C.α=200rad/s2,顺时针向D. α==200rad/s2,逆时针向
半径R=10cm的鼓轮,由挂在其上的重物带动而绕O轴转动,如图所示。重物的运动方程为x= 100t2(x以m计,t以s计)。则鼓轮的角加速度α的大小和方向是:
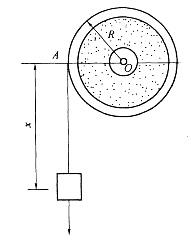

A.α=2000rad/s2,顺时针向
B. α==2000rad/s2,逆时针向
C.α=200rad/s2,顺时针向
D. α==200rad/s2,逆时针向
B. α==2000rad/s2,逆时针向
C.α=200rad/s2,顺时针向
D. α==200rad/s2,逆时针向
参考解析
解析:提示:重物的加速度即是轮缘的切向加速度。
相关考题:
质量为m,半径为R的均质圆轮,绕垂直于图面的水平轴O转动,其角速度为w。在图示瞬时,角加速度为0,轮心C在其最低位置,此时将圆轮的惯性力系向O点简化, 其惯性力主矢和惯性力主矩的大小分别为:
半径R=10cm的鼓轮,由挂在其上的重物带动而绕O轴转动,如图所示。重物的运动方程为x= 100t2(x以m计,t以s计)。则鼓轮的角加速度α的大小和方向是:A.α=2000rad/s2,顺时针向B. α==2000rad/s2,逆时针向C.α=200rad/s2,顺时针向D. α==200rad/s2,逆时针向
图示两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r,并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m,对轴O的回转半径为ρ0外。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为ρO。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
小车沿水平方向向右做加速运动,其加速度a0=49.2cm/s2,在小车上有一轮绕O轴转动,转动规律为φ=t2(t以秒计,φ以弧度计)。当t=1s时.轮缘上点A的位置如图所示。如轮的半径r=20cm,求此时点A的绝对加速度aA为( )cm/s2。A.24.7B.43.5C.68.2D.74.6
两重物的质量均为m,分别系在两软绳上,此两绳又分别绕在半径各为r与2r并固结一起的两圆轮上,两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为p0,两重物中一铅垂悬挂,一置于光滑平面上,当系统在左重物重力作用下运动时,鼓轮的角加速度a为:
图示鼓轮半径r=3.65m,对转轴O的转动惯量JO= 0.92kg ? m2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:A. 37.8N ? m B. 47N ? mC. 36.3N ? m D. 45.5N ? m
物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)此物体内,转动半径r=0.5m的一点在to=0时的速度和法向加速度的大小为()。A.2 m/s,8 m/s2B.3 m/s,3 m/s2C.2 m/s,8.54m/s2D.0.8 m/s2
点M在曲线AOB上运动。曲线由AO、OB两段圆弧组成。AO段曲率半径R1=18m,OB段曲率半径R2=24m,取两圆弧交接点O为原点,并规定正负方向如图示。已知点M的运动方程为s=3+4t-t2(t以秒计,s以米计),则t=5秒时点M的加速度大小为()。A、1.5m/s2B、2m/s2C、2m/s2D、4m/s2
单选题(2012)物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)此物体内,转动半径r=0.5m的一点,在t0=0时的速度和法向加速度的大小分别为:()A2m/s,8m/s2B3m/s,3m/s2C2m/s,8.54m/s2D0,8m/s2
单选题物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)。此物体内,转动半径r=0.5m的一点,在t0=0时的速度和法向加速度的大小为( )。[2012年真题]A2m/s,8m/s2B3m/s,3m/s2C2m/s,8.54m/s2D0,8m/s2
单选题图示鼓轮半径r=3.65m,对转轴O的转动惯量Jo=0.92kg·m 2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:()A 37.8N.mB 47N.mC 36.3N.mD 45.5N.m