高考数学复习专题23《利用导数证明不等式》讲义及答案
设R(t)表示可靠度函数,F(t)表示累积故障分布函数,则下列表述正确的有( )。
A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1
B.R(t)是[0,∞)区间内的非增函数,且0≤R(t)≤1
C.在[0,∞)区间内,R(t)+F(t)=1
D.F(t)在[0,∞)区间内的非减函数,且0≤F(t)≤1
E.F(t)在[0,∞)区间内是非增函数
解析:可靠度R(t)随时间推移越来越低,是[0,∞)区间内的非增函数,且0≤R(t)≤1;而F(t)是[0,∞)区间内的非减函数,且0≤F(t)≤1;在[0,∞)区间内,R(t)+F(t)=1。
设定义域在R上的函数f(x)=x|x|,则f(x)是
A.奇函数,增函数
B.偶函数,增函数
C.奇函数,减函数
D.偶函数,减函数
设定义域在R上的函数,f(x)=x|x|,则f(x)是
A.奇函数,增函数
B.偶函数,增函数
C.奇函数,减函数
D.偶函数,减函数
已知公差为2的正整数等差数列为an,则该数列满足不等式7/16<an/5<398/9的所有项的和为( )
A.12320
B.12430
C.12432
D.12543
13.【解析】公差为2的正整数数列为奇数列,满足条件的an最小为3,最大为221,故和为(3+221)×[(221-3)÷2+1]。故选A。
专题23 利用导数证明不等式一、多选题 1已知函数,数列的前n项和为,且满足,则下列有关数列的叙述正确的是( )ABCD2下列不等式正确的是( )A当时,B当时,C当时,D当时,3已知定义在R上的函数满足,则下列式子成立的是( )ABC是R上的增函数D,则有二、解答题4已知函数,若最小值为0.(1)求实数的值;(2)设,证明:.5已知函数,.(1)当时,求函数的最大值;(2)设,当,且,求证:.6已知函数,其中为自然对数的底数(1)当时,证明:;(2)设实数,是函数的两个零点,求实数的取值范围7已知,当时恒成立(1)求实数的取值范围;(2)当时,求证:8已知函数.(1)当时,求曲线在点处的切线方程;(2)若,求证:.9已知函数.(1)若只有一个极值点,求的取值范围.(2)若函数存在两个极值点,记过点的直线的斜率为,证明:.10函数.(1)当时,求的单调区间;(2)当,时,证明:.11已知函数(1)讨论函数的单调区间;(2)当时,求证:12函数.(1)若,求的单调性;(2)当时,若函数有两个零点,求证:.13已知函数(1)试讨论的单调性;(2)若,证明:14已知函数.(1)当时,求的最小值;(2)若对任意恒有不等式成立.求实数的值;证明:.15已知a0,函数(1)若f(x)为减函数,求实数a的取值范围;(2)当x1时,求证:(e2.718)16已知函数,.(1)判断函数的单调性;(2)若,判断是否存在实数,使函数的最小值为2?若存在求出的值;若不存在,请说明理由;(3)证明:.17已知函数.(1)求证:;(2)函数,有两个不同的零点,.求证:.18已知函数,.(1)若函数在区间内是增函数,求的取值范围;(2)证明:.19已知函数.(1)若a= -2,求函数f(x)的单调区间;(2)若函数f(x)有两个极值点x1,x2,求证.20(1)当时,求证:;(2)若对于任意的恒成立,求实数k的取值范围;(3)设a0,求证;函数在上存在唯一的极大值点,且.专题23 利用导数证明不等式一、多选题 1已知函数,数列的前n项和为,且满足,则下列有关数列的叙述正确的是( )ABCD【答案】AB【分析】A计算出的值,与比较大小并判断是否正确;B利用导数分析的最小值,由此判断出是否正确;C根据与的大小关系进行判断;D构造函数,分析其单调性和最值,由此确定出,将变形可得,再将变形可判断结果.【详解】A选项,A正确;B选项,因为,所以当时,所以单增,所以,因为,所以,所以,B正确;C选项,因为,所以,C错误;D选项,令,所以在单调递增,所以,所以,则,所以,即,所以,所以D错误.故选:AB.【点睛】易错点睛:本题主要考查导数与数列的综合问题,属于难题.解决该问题应该注意的事项:(1)转化以函数为背景的条件时,应该注意题中的限制条件,如函数的定义域,这往往是很容易被忽视的问题;(2)利用函数的方法研究数列中的相关问题时,应准确构造相应的函数,注意数列中相关限制条件的转化.2下列不等式正确的是( )A当时,B当时,C当时,D当时,【答案】ABC【分析】构建函数,利用导数研究其单调性和最值,可得出每个选项中的不等式正不正确.【详解】对于A:设,则,令,解得,当时函数单调递减,当时,函数单调递增,所以函数在时,函数取得最小值,故当时,故A正确;对于B:设,所以,令,解得,当时,函数单调递增,当时,函数单调递减,所以在时,(1),故当时,恒成立,故B正确;对于C:设,所以,令,解得,当时,函数单调递减,当时,函数单调递增,所以当时,(1),所以当时,故C正确;对于D:设函数,则,所以是定义在上单调递增的奇函数,所以时,成立,时,故D错误故选:ABC3已知定义在R上的函数满足,则下列式子成立的是( )ABC是R上的增函数D,则有【答案】AD【分析】由题意得,即为增函数,可得,即可判断,举出反例可判断C,根据单调性可判断D.【详解】由,得,即,所以函数为增函数,故,所以,故A正确,B不正确;函数为增函数时,不一定为增函数,如是增函数,但是减函数,所以C不正确;因为函数为增函数,所以时,有,故有成立,所以D正确.故选:AD.【点睛】本题主要考查了利用导数判断函数的单调性,构造函数是解题的关键,属于中档题.二、解答题4已知函数,若最小值为0.(1)求实数的值;(2)设,证明:.【答案】(1)1;(2)证明见解析.【分析】(1)由,得,讨论当时,无最小值.当时, ,由可得答案得;(2)由(1)可知,可得,由(1)可知,即,进而可得结论.【详解】(1)由已知,定义域为.由,得.当时,在单调递增无最小值.当时,;,.故,令,.,;,所以由,得.(2)由(1)可知,此时等价于,由(1)可知当时,.故,即.所以,故.【点睛】不等式证明问题是近年高考命题的热点,利用导数证明不等主要方法有两个,一是比较简单的不等式证明,不等式两边作差构造函数,利用导数研究函数的单调性,求出函数的最值即可;二是较为综合的不等式证明,要观察不等式特点,结合已解答的问题把要证的不等式变形,并运用已证结论先行放缩,然后再化简或者进一步利用导数证明.5已知函数,.(1)当时,求函数的最大值;(2)设,当,且,求证:.【答案】(1);(2)证明见解析.【分析】(1)当时,由的单调性得出函数的最大值;(2)由函数的单调性结合零点个数得出,结合分析法要证,只需证,由函数在上存在唯一零点证明,由函数在上存在唯一零点证明,从而得出.【详解】解1)当时,.当时,;当时,.函数在上单调递增,在上单调递减.(2)由题可知,是函数的零点.当时,;当时,函数在上单调递增,在上单调递减故函数要有两个零点,必有,即.要证,只需证只需证 由于,函数在上存在唯一零点即. 由(1)知,所以,且当时,取等号函数在上存在唯一零点即. 由可知成立,故.【点睛】求解本题第(2)问的关键是根据题中条件将证明转化为证明,然后利用零点存在定理即可求解.6已知函数,其中为自然对数的底数(1)当时,证明:;(2)设实数,是函数的两个零点,求实数的取值范围【答案】(1)证明见解析;(2)【分析】(1)构造函数,证明最小值大0即可得解;(2)先求导可,分,和进行讨论即可得解.【详解】(1)设,在上单调递增,又,时,在上单调递增,又,时,故当时,(2),当时,易知函数只有一个零点,不符合题意当时,在上,单调递减;在上,单调递增;又,不妨取且时,或者考虑:当,所以函数有两个零点,符合题意,当时,由得或()当,即时,在上,成立,故在上单调递增,所以函数至多有一个零点,不符合题意()当,即时,在和上,单调递增;在上,单调递减;又,且,所以函数至多有一个零点,不符合题意()当即时,在和上,单调递增;在上,单调递减,以,所以函数至多有一个零点,不符合题意综上所述,实数的取值范围是【点睛】本题考查了导数的应用,考查了利用导数研究函数的单调性,考查了构造法证明不等式以及分类讨论求参数范围,要求较高的计算能力,属于难题.解决本类问题的方法有以下几点:(1)证明题常常利用构造法,通过构造函数来证明;(2)分类讨论解决含参问题,是导数压轴题常考题型,在讨论时重点是找到讨论点.7已知,当时恒成立(1)求实数的取值范围;(2)当时,求证:【答案】(1);(2)证明见解析.【分析】(1)移项构造函数,求导后分类讨论.(2)利用(1)的结论构造新函数,求导后构造新函数再求导寻找极值点即可.【详解】(1)即恒成立,令,则当时,则在是增函数,成立当时,使,为减函数,为增函数所以不合题意所以(2)由(1)得当时,所以要证只要证即证:,设,所以在是增函数,所以存在使故时,则为减函数,时则为增函数,所以时,故命题成立【点睛】此题为导数综合题,属于难题.方法点睛:利用导数求参数范围方法:(1)变量分离,构造函数,转化为恒成立问题处理,求导数进步求新函数的最值.(2)移项后,构造函数,求导讨论函数的单调性及极值.8已知函数.(1)当时,求曲线在点处的切线方程;(2)若,求证:.【答案】(1);(2)证明见解析.【分析】(1)首先求导得到,从而得到,再利用点斜式求切线方程即可.(2)首先求导得到,根据在上单调递增,且,且,得到存在唯一,使得,再根据函数的单调性得到,利用基本不等式即可证明.【详解】(1)当时,.,又,在点处的切线方程为,即.(2),易知在上单调递增,且,又,存在唯一,使得,即.当时,为减函数;当时,为增函数.当且仅当,即时,等号成立.当时,.【点睛】关键点点睛:本题主要考查导数的综合应用,考查利用导数证明不等式,解题的关键为找到导函数的隐藏零点,属于中档题.9已知函数.(1)若只有一个极值点,求的取值范围.(2)若函数存在两个极值点,记过点的直线的斜率为,证明:.【答案】(1);(2)证明见解析.【分析】(1)先求导,令,则.令,解不等式组即得解;(2)只需证,设,函数,证明即得证.【详解】(1)解:,令,则.令,要使函数只有一个极值点,则需满足,即;(2)证明:因为,所以,因为存在两个极值点,所以即 不妨假设,则 要证,即要证,只需证, 只需证,即证 设,函数, 因为,故,所以,即,故在上单调递减,则 又因为,所以,即,从而得证.【点睛】关键点点睛:解答本题的关键是通过分析得到只需证明.对于比较复杂的问题,我们可以通过分析把问题转化,再证明,提高解题效率.10函数.(1)当时,求的单调区间;(2)当,时,证明:.【答案】(1)单调递减区间为,单调递增区间为;(2)证明见解析.【分析】(1)由得到 求导由, 求解. (2)求导,分,讨论求解.【详解】(1)当时, ,.所以当时,;当时,.所以的单调递减区间为,单调递增区间为.(2)因为,所以.当,时,恒成立,所以单调递增,所以,而,所以恒成立;,时,由可得;由可得.所以在单调递减,
设R(t)表示可靠度函数,F(t)表示累积故障分布函数,则以下表述正确的是( )。
A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1
B.R(t)是[0,∞]区间内的非增函数,且0≤R(t)≤1
C.在(0,∞)区间内,R(t)+F(t)=1
D.F(t)在[0,∞]区间内的非减函数,且0≤F(t)≤1
E.F(t)在[0,∞]区间内是非增函数
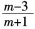
则m的取值范围是( )。
B.m>1或m<-3
C.-1<m<3
D.m>3或m<-1



B.已知逻辑函数A+B=A+C,则B=C
C.已知逻辑函数AB=AC,则B=C
D.已知逻辑函数A+B=A,则B=1
A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1
B.R(t)是[0, ∞)区间内的非增函数,且0≤R(t)≤1
C.在[0,∞)区间内,R(t) +F(t) =1
D. F(t)在[0,∞)区间内的非减函数,且0≤F(t)≤1
E.F(t)在[0,∞)区间内是非增函数
相关考题:
- 出票人在支票上的签章,必须与预留银行印鉴相符。
- 国防是一个庞大的系统工程,国防强固必须优化各相关要素,包括( )、( )、( )、( )、( )、( )、( )、( )。A.政治清明,经济实力雄厚B.武装力量强大C.全民爱国,关心国防D.实行进攻性的军事战略E.国防科技工业先进配套F.国防工程设施完善G.建立广泛的国际联盟H.国防动员体制机制先进有效
- 空降兵不属于什么军种? A.海军 B.陆军 C.火箭军 D.空军
- 银行账务组织包括哪些内容?各项内容之间的关系如何?
- 在托收承付结算中,付款人在承付期内提出拒付,银行应审查其拒付理由.
- ( 难度:中等)Kafka消费者偏移量有几种控制方法A.自动提交B.半自动提交C.手动提交D.随机提交
- 当贷款的本金或利息逾期 90 天时,应单独核算。
- ( 难度:中等)以下哪种不是Hive支持的数据类型A.longB.xmlC.IntD.string
- ( 难度:中等)关于参数传递说法正确的()A.A:基本数据类型参数传递的是值,引用数据类型参数传递的是引用B.B:不管是基本数据类型还是引用数据类型都是值传递C.C:基本数据类型参数传递的是数据值,引用数据类型参数传递的是对象D.D:基本数据类型参数是值传递,引用数据类型传递是引用传递
- ( 难度:中等)Hive适用于以下哪些应用场景A.统计上个月在网用户数B.计算近十年人均话费变化趋势C.实时计算用户套餐剩余量D.疫情期计算用户行程数据