2022年甘肃省兰州市中考数学试题(含答案解析)
两个变量(x,y),其观测值为,(x1,y1)(z2,Y2),2,…,n,若回归方程为,y=a+bx则下列表述正确的是( )。
A.回归直线经过点(0,0)
B.回归直线经过点
C.回归直线经过点(1,a)
D.以上都不正确
A、一定
B、不一定
A.直线垂直于平面
B.直线必定在平面内
C.直线与平面成斜交
D.直线必定在平面外
A、若空间一直线与平面平行,则此直线与该平面上任何直线都平行
B、若空间一直线与平面平行,则在该平面上只能找出一条直线与该直线平行
C、若空间一直线与平面上任一直线平行,则此直线与该平面平行
D、若空间一直线与一迹线平面平行,则此直线必与该平面上的一条迹线平行
A.倾斜于投影
B.反映实长
C.积聚为点
D.平行于投影轴
2022年甘肃省兰州市中考数学试题一、选择题1. 计算的结果是( )A. 2B. 2C. D. 2. 如图,直线,直线c与直线a,b分别相交于点A,B,垂足为C若,则( )A. 52B. 45C. 38D. 263. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A. B. C. D. 4. 计算:( )A. B. C. D. 5. 如图,内接于,CD是的直径,则( )A. 70B. 60C. 50D. 406. 若一次函数的图象经过点,则与的大小关系是( )A. B. C. D. 7. 关于x的一元二次方程有两个相等的实数根,则( )A. -2B. -1C. 0D. 18. 已知,若,则( )A. 4B. 6C. 8D. 169. 无色酚酞溶液是一中常见常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色现有5瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )A. B. C. D. 10. 如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,则( )A 4B. C. 2D. 11. 已知二次函数,当函数值y随x值的增大而增大时,x的取值范围是( )A. B. C. D. 12. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角形成的扇面,若,则阴影部分的面积为( )A. B. C. D. 二、填空题13. 因式分解:_14. 如图,小刚在兰州市平面地图的部分区域建立了平面直角坐标系,如果白塔山公园的坐标是(2,2),中山桥的坐标是(3,0),那么黄河母亲像的坐标是_15. 如图,在矩形纸片ABCD中,点E在BC边上,将沿DE翻折得到,点F落在AE上若,则_cm16. 2022年3月12日是我国第44个植树节,某林业部门为了考察某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:幼树移植数(棵)100100050008000100001500020000幼树移植成活数(棵)878934485722489831344318044幼树移植成活的频率0.87008930.8970.9030.8980.8960.902估计该种幼树在此条件下移植成活概率是_(结果精确到0.1)三、解答题17. 解不等式:18. 计算:19. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,求的大小20. 如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高1.5m的测角仪DE测得,然后沿EB方向向前走3m到达点G处,在点G处用高1.5m的测角仪FG测得求凉亭AB的高度(A,C,B三点共线,结果精确到0.1m)(参考数据:,)21. 人口问题是“国之大者”以习近平同志为核心的党中央高度重视人口问题,准确把握人口发展形势,有利于推动社会持续健康发展,为开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军创造良好的条件某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:信息一:普查登记的全国大陆31个省、自治区、直辖市人口数的频数分布直方图如下:(数据分成6组:,)信息二:普查登记的全国大陆31个省、自治区、直辖市人口数(百万人)在这一组的数据是:58,47,45,40,43,42,50;信息三:20102021年全国大陆人口数及自然增长率;请根据以上信息,解答下列问题:(1)普查登记的全国大陆31个省、自治区、直辖市人口数的中位数为_百万人(2)下列结论正确的是_(只填序号)全国大陆31个省、自治区、直辖市中人口数大于等于100(百万人)的有2个地区;相对于2020年,2021年全国大陆人口自然增长率降低,全国大陆人口增长缓慢;2010-2021年全国大陆人口自然增长率持续降低(3)请写出2016-2021年全国大陆人口数、全国大陆人口自然增长率的变化趋势,结合变化趋势谈谈自己的看法22. 综合与实践问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎范、芯组成的(如图1),它的端面是圆形,如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到,在圆上标记A,B,C三点;将“矩”向右旋转,使它左侧边落在A,B点上,“矩”的另一条边与圆的交点标记为D点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,连接AD,BC相交于点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,链接AD,BC相较于点O,即O为圆心(1)问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O如图3,点A,B,C在上,且,请作出圆心O(保留作图痕迹,不写作法)(2)类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O如图4,点A,B,C在上,请作出圆心O(保留作图痕迹,不写作法)(3)拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差如图5,点A,B,C是上任意三点,请用不带刻度的直尺和圆规作出圆心O(保留作图痕迹,不写作法)请写出你确定圆心的理由:_23. 如图,在中,M为AB边上一动点,垂足为N设A,M两点间的距离为xcm(),B,N两点间的距离为ycm(当点M和B点重合时,B,N两点间的距离为0)小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究下面是小明的探究过程,请补充完整(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,得到了y与x的几组对应值:x/cm00.511.51.822.533.544.55y/cm43.963.793.47a2.992.401.791.230.740.330请你通过计算,补全表格:_;(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点,并画出函数y关于x的图像;(3)探究性质:随着自变量x的不断增大,函数y的变化趋势:_(4)解决问题:当时,AM长度大约是_cm(结果保留两位小数)24. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处(1)求y关于x的函数表达式;(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分该女生在此项考试中是否得满分,请说明理由25. 如图,点A在反比例函数的图像上,轴,垂足为,过作轴,交过B点的一次函数的图像于D点,交反比例函数的图像于E点,(1)求反比例函数和一次函数的表达式:(2)求DE的长26. 如图,是的外接圆,AB是直径,连接AD,AC与OD相交于点E(1)求证:AD是的切线;(2)若,求的半径27. 在平面直角坐标系中,是第一象限内一点,给出如下定义:和两个值中的最大值叫做点P的“倾斜系数”k(1)求点的“倾斜系数”k的值;(2)若点的“倾斜系数”,请写出a和b的数量关系,并说明理由;若点的“倾斜系数”,且,求OP的长;(3)如图,边长为2的正方形ABCD沿直线AC:运动,是正方形ABCD上任意一点,且点P的“倾斜系数”,请直接写出a的取值范围28. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点,EP与正方形的外角的平分线交于P点试猜想AE与EP的数量关系,并加以证明;(1)【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题请在图1中补全图形,解答老师提出的问题(2)【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合),是等腰直角三角形,连接CP,可以求出的大小,请你思考并解答这个问题(3)【拓展迁移】突击小组深入研究希望小组提出这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合),是等腰直角三角形,连接DP知道正方形的边长时,可以求出周长的最小值当时,请你求出周长的最小值2022年甘肃省兰州市中考数学试题答案解析一、选择题1. B【详解】4的算术平方根是2,即=2,2. C【详解】解:ab,1=ABC=52,ACb,ACB=90,2=90-ABC=38,3. D详解】解:A不能沿一条直线折叠完全重合;B不能沿一条直线折叠完全重合;C不能沿一条直线折叠完全重合;D能够沿一条直线折叠完全重合;4. A【详解】解:原式=5. C【详解】解:CD是O的直径,CAD90,ACD+D90,ACD40,ADCB506. A【详解】解:一次函数y=2x+1中,k=20,y随着x的增大而增大点(-3,y1)和(4,y2)是一次函数y=2x+1图象上的两个点,-34,y1y27. B【详解】原方程有两个相等的实数根,b24ac44(k)0,且k0;解得8. A【详解】解:,即,解得9. B【详解】解:酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色,总共有5种溶液,其中碱性溶液有2种,将酚酞试剂滴入任意一瓶液体后呈现红色概率是:10. C【详解】是菱形,E为AD的中点,是直角三角形,即,11. B【详解】解:开口向上,对称轴为x=1,x1时,函数值y随x的增大而增大12. D【详解】解:S阴影=S扇形AOD-S扇形BOC=2.25(m2)二、填空题13. 【答案】【详解】解:原式,14. 【答案】【详解】解:如图,根据白塔山公园的坐标是(2,2),中
A.永远是直线
B.积聚为点
C.与投影轴平行的直线
D.直线
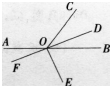
直线AB,CD相交于点O。
(1)OE,OF分别是∠AOC,∠BOD的平分线。画出这个图形。
(2)射线OE,OF在同一条直线上吗?
(3)画∠AOD的平分线OG。OE与OG有什么位置关系?
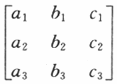 是满秩的,则直线
是满秩的,则直线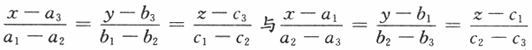
B.重合
C.平行但不重合
D.异面

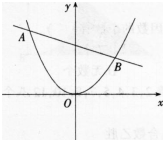
(1)直线ι经过一个定点C,试求出点C的坐标;(2分)
(2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)


B.45o
C.60o
D.90o
相关考题:
- 名词解释题中央银行票据
- 名词解释题同业拆借市场
- 多选题患者女性,46岁,对称性多关节肿痛1年,加重3月入院。患者1年前无明显原因出现双手近端指间关节、掌指关节、双腕关节肿痛,伴有晨僵,每天可持续>1小时,自行口服"双氯芬酸片、泼尼松片"症状可好转,未规律治疗。近3月,出现双肘关节,双足跖趾关节肿痛,以上关节肿痛加重,并出现双肘、枕部皮下结节。为进一步诊治来我院。起病以来,伴有口干、眼干,精神食欲差,睡眠差。既往史、个人史、月经婚育史无特殊。家族史中其母患有类风湿关节炎。体格检查:血压130/76mmHg心肺腹无特殊阳性体征。双肘、枕部皮肤可触及皮下结节,质硬,无压痛。左手第2、3、4近端指间关节、右手第3、5近端指间关节呈梭形肿胀,左2、3、4掌指关节、右3、4、5掌指关节、双腕关节肿胀,压痛(+),双肘关节活动受限,左足第二跖趾关节肿胀,双下肢无水肿。辅助检查血常规:白细胞5.1×109/L,血红蛋白96g/L,血小板538×109/L;血沉76mm/h,CRP0.27mg/dl。适宜的治疗措施有()。A应用非甾体抗炎药,如美洛昔康、赛来昔布等B活动期应注意休息,缓解期应加强关节锻炼C小剂量的皮质类固醇,如泼尼松10~20mg/dD注意建立长期治疗的观念,定期去医院检查E单独或联合应用免疫抑制剂如甲氨蝶呤、羟氯喹、柳氮磺吡啶、CTX等。
- 多选题患者,女,78岁。腰背疼痛3年,加重10天,伴乏力,有时全身疼痛,晚间亦病痛,轻度影响睡眠。10天前,按摩后腰背疼痛加重,严重影响睡眠。查体:老年女性,"驼背",胸腰椎多处叩击痛(+),椎旁压痛(±),双上下肢无异常,X线示T12陈旧性压缩骨折。既往高血压病史20年,否认糖尿病病史。椎体成形术可用以下哪些治疗()A椎体肿瘤B骨质疏松症椎体压缩性骨折C多发性骨髓瘤椎体病理骨折D症状性椎体血管瘤E椎体滑脱致椎体不稳F椎体转移瘤引起顽固性疼痛
- 问答题期货交易的特点
- 多选题下列物权中,属于用益物权的有()。A土地承包经营权B建设用地使用权C抵押权D地役权
- 钢筋焊接接头拉伸试验时,3个试件均断于热影响区,呈延性断裂,抗拉强度大于钢筋母材抗拉强度标准值,应进行复检。
- Staff Management: the importance of encouraging staff to make suggestions for improvements
- 烧结空心砖和空心砌块(GB13545-2003)标准中规定,砖和砌块产品中不允许有欠火砖、酥砖。
- 多选题患者,男,65岁。因反复右下肢疼痛1个月余来诊,诉疼痛自右臀部沿大腿后侧下行放射至小腿后外侧,行走疼痛加重,夜间著,无麻木感。患者2个月前曾查体发现肝癌行手术治疗。查体腰椎无明显压痛,双侧直腿抬高试验阴性,右臀部坐骨神经出口处压痛。门诊行坐骨神经阻滞后,疼痛立刻缓解,2天后疼痛渐出现,1周后复诊诉仍有疼痛,但较前有所减轻,要求进一步处理。呼吸抑制是阿片类药物最严重的不良反应,其特点为()A临床主要表现为呼吸频率降低(8次/分)和动脉氧饱和度下降B疼痛的病人不会发生呼吸抑制C逐渐增加阿片药剂量可减少呼吸抑制的发生D肾功能不全患者应适当减少阿片药物用量,可降低呼吸抑制发生E一旦发现呼吸频率下降,应立即使用纳洛酮解救
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(95)-
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(第12卷)-
- 2022年时政100题(含答案)-
- 一年级语文下册按课文内容填空(附答案)-
- 2020年秋武汉理工大学《财务管理》在线练习题库_
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(72)-
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(52)-
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(第10版)-
- 其他生产经营单位-主要负责人安全生产考试试题测试强化卷及答案(第20卷)-
- 2018年教师编制考试招聘必考知识点整理-