沿x轴正向传播平面单色电磁波为( )。
沿x轴正向传播平面单色电磁波为( )。


参考解析
解析: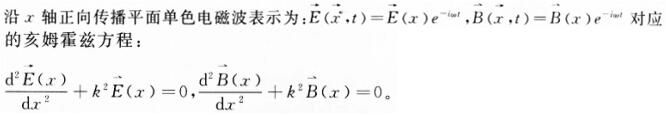
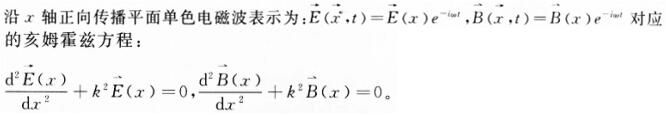
相关考题:
一平面谐波以u的速率沿x轴正向传播,角频率为ω,那么,距原点x处(x>0)质点的振动相位与原点处质点的振动相位相比,具有的关系是( )。A.滞后ωx/uB.滞后x/uC.超前ωx/uD.超前x/u
一列简谐横波在t1=0.5 S时的波形图如图所示。已知平衡位置在x=0.5 m的A处的质点,在t2=1.5s时第一次回到A处,且其速度方向指向y轴负方向。这列波(??)A.沿x轴正向传播,波速为1 m/sB.沿x轴正向传播,波速为2 m/sC.沿x轴负向传播,波速为1 m/sD.沿x轴负向传播,波速为2 m/s
一列简谐横波沿x轴传播,t=0时刻的波形如图4所示,则从图中可以看出()。A.这列波的波长为5mB.波中的每个质点的振动周期为4SC.若已知波沿x轴正向传播.则此时质点a向下振动D.若已知质点b此时向上振动,则波是沿x轴负向传播的
一平面简谐波沿x轴正向传播,已知x=L(Lλ)处质点的振动方程为y=Acosωt,波速为u,则波动方程为()A、y=Acosω[t-(x-L)/u]B、y=Acosω[t-(x+L)/u]C、y=Acosω[t+(x+L)/u]D、y=Acosω[t+(x-L)/u]
平面内作用于同一点的四个力若以力的作用点为坐标原点,有F1=5N,方向沿x轴的正向;F2=6N,沿y轴正向;F3=4N,沿x轴负向;F4=8N,沿y轴负向,以上四个力的合力方向指向()A、第一象限B、第二象限C、第三象限D、第四象限
一平面简谐波沿X轴正向传播,已知x=L(Lλ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为()。A、y=Acosω(t+L/u)B、y=Acosω(t-L/u)C、y=Acos(ωt+L/u)D、y=Acos(ωt-L/u)
一平面谐波以u的速率沿x轴正向传播,角频率为w。那么,距原点x处(x0)质点的振动相位与原点处质点的振动相位相比,有下列哪种关系?()A、滞后wx/uB、滞后x/uC、超前wx/uD、超前x/u
一平面简谐波沿x轴正向传播,已知x=-5m处质点的振动方程为y=Acosπt,波速为u=4m/s,则波动方程为:()A、y=Acosπ[t-(x-5)/4]B、y=Acosπ[t-(x+5)/4]C、y=Acosπ[t+(x+5)/4]D、y=Acosπ[t+(x-5)/4]
一平面谐波以u的速率沿x轴正向传播,角频率为ω。那么,距原点x处(x0)质点的振动相位与原点处质点的振动相位相比,有下列哪种关系()?A、滞后ωx/uB、滞后x/uC、超前ωx/uD、超前x/u
单选题一平面谐波以u的速率沿x轴正向传播,角频率为w。那么,距原点x处(x0)质点的振动相位与原点处质点的振动相位相比,有下列哪种关系?()A滞后wx/uB滞后x/uC超前wx/uD超前x/u
单选题一平面简谐波沿X轴正向传播,已知x=L(Lt,波速为u,那么x=0处质点的振动方程为()。Ay=Acosω(t+L/u)By=Acosω(t-L/u)Cy=Acos(ωt+L/u)Dy=Acos(ωt-L/u)
单选题一平面简谐波沿z轴正向传播,已知x=L(Lλ)处质点的振动方程为Y=Acoswt,波速为u,那么x=0处质点的振动方程为()。Ay=Acos(wt+L/u)By=Acos(wt-L/u)Cy=Acosw(t+L/u)Dy=Acosow(t-L/u)
单选题一平面简谐波沿X轴正向传播,已知x=L(L0),波速为u,那么x=0处质点的振动方程为:()Ay=Acos[ω(t+L/u)+φ0]By=Acos[ω(t-L/u)+φ0]Cy=Acos[ωt+L/u+φ0]Dy=Acos[ωt-L/u+φ0]
单选题一平面简谐波沿x轴正向传播,已知x=L(Lλ)处质点的振动方程为y=Acosωt,波速为u,则波动方程为()Ay=Acosω[t-(x-L)/u]By=Acosω[t-(x+L)/u]Cy=Acosω[t+(x+L)/u]Dy=Acosω[t+(x-L)/u]
单选题测量学中,高斯平面直角坐标系X轴、Y轴的定义为( )。[2012年真题]AX轴正向为东,Y轴正向为北BX轴正向为西,Y轴正向为南CX轴正向为南,Y轴正向为东DX轴正向为北,Y轴正向为东