一定量的理想气体贮于某一容器中,温度为T,气体分子的质量为m,根据理想气体的分子模型和统计假设,分子速度在x方向的分量平方的平均值( )。
一定量的理想气体贮于某一容器中,温度为T,气体分子的质量为m,根据理想气体的分子模型和统计假设,分子速度在x方向的分量平方的平均值( )。
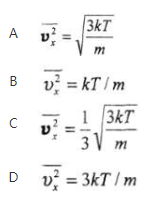
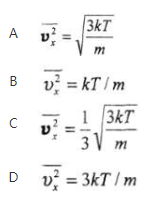
参考解析
解析:
相关考题:
若理想气体的体积为V,压强为p,温度为T,每个分子的平均分子量为M,k为玻尔兹曼常数,R为摩尔气体常量,则该理想气体的分子数为( )。A.pV/mB.pV/(kT)C.pV/(RT)D.pV/(mT)
若理想气体的体积为V,压强为p,温度为T, 一个分子的质量为m,k为玻耳兹曼常量,R为摩尔气体常量,则该理想气体的分子数为( )。A. pV/m B. pV/(kT) C. pV/(RT) D. pV/(mT)
一容器内贮有理想气体,压强为1.33Pa,温度为7℃,在平衡状态下,则单位体积(1m3)中的分子数为()。A、2.40×1020m-3B、2.50×1022m-3C、3.45×1020m--3D、3.65×1021m-3
关于理想气体下列说法错误的是()A、1克分子的理想气体的体积为22.4升B、在标准状态下,1克分子的理想气体的质量为其分子量C、理想气体在任何情况下都能无条件地遵守玻意耳(Boyle)定律、盖-吕萨克(GayLussac)和查理(Charles)定律D、一般气体,在压强不太大(与标准大气压相比)、温度不太高(与室温相比)的状态下,可看成是理想气体
单选题若理想气体的体积为V,压强为p,温度为T,每个分子的平均分子量为M,k为玻尔兹曼常数,R为摩尔气体常量,则该理想气体的分子数为( )。ApV/MBpV/(kT)CpV/(RT)DpV/(MT)
单选题若理想气体的体积为V,压强为p,温度为T,一个分子的质量为m,k为玻兹曼常量,R为摩尔气体常量,则该理想气体的分子数为()。ApV/mBpv/(kT)CpVr/(RT)DPv/(mT)