平面四连杆机构ABCD如图所示,如杆AB以等角速度ω= 1rad/s绕A轴顺时针向转动,则CD杆角速度ωCD的大小和方向为:A. ωCD= 0. 5rad/s,逆时针向B. ωCD= 0. 5rad/s,顺时针向C. ωCD= 0. 25rad/s,逆时针向D. ωCD= 0. 25rad/s,顺时针向
平面四连杆机构ABCD如图所示,如杆AB以等角速度ω= 1rad/s绕A轴顺时针向转动,则CD杆角速度ωCD的大小和方向为:
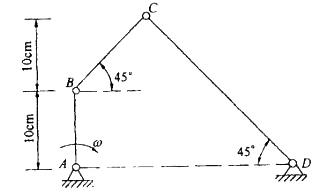

A. ωCD= 0. 5rad/s,逆时针向
B. ωCD= 0. 5rad/s,顺时针向
C. ωCD= 0. 25rad/s,逆时针向
D. ωCD= 0. 25rad/s,顺时针向
B. ωCD= 0. 5rad/s,顺时针向
C. ωCD= 0. 25rad/s,逆时针向
D. ωCD= 0. 25rad/s,顺时针向
参考解析
解析:提示:CB平面运动,速度投影定理。
相关考题:
曲柄机构在其连杆AB的中点C与CD杆铰接,而CD杆又与DF杆铰接,DE杆可绕E点转动。曲柄OA以角速度ω= 8rad/s绕O点逆时针向转动。且OA = 25cm,DE=100cm。在图示瞬时,O、A、B三点共在一水平线上,B、E两点在同一铅直线上,∠CDE=90°,则此时DE杆角速度ωDE的大小和方向为:
平面四连杆机构ABCD如图所示,如杆AB以等角速度ω=1rad/s绕A轴顺时针向转动,则CD杆角速度ωCD的大小和方向为( )。A.ωC.D.=005rA.D./s,逆时针向B.ωC.D.=05rA.D./s,顺时针向C.ωC.D.=025rA.D./s,顺时针向D.ωC.D.=025rA.D./s,逆时针向
图示凸轮机构,凸轮以等角速度ω绕通过O点且垂直于图示平面的轴转动,从而推动杆AB运动。已知偏心圆弧凸轮的偏心距OC=e,凸轮的半径为r,动系固结在凸轮上,静系固结在地球上,则在图示位置()杆AB上的A点牵连速度的大小等于( )。
均质细直杆AB长为l,质量为m,以匀角速度ω绕O轴转动,如图4-69所示, 则AB杆的动能为( )。