阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子(即N的约数以及1,但不包括N)之和S,则称该数为“完美数”。例如6=1+2+3,28=1+2+4+7+14,所以6和28都是完美数。显然,6是第1个(即最小的)完美数。下面流程图的功能是求500以内所有的完美数。【流程图】循环开始框中要注明:循环变量=初始值,终值[,步长],步长为1时可以缺省。如果某自然数小于其所有真因子之和(例如24<1+2+3+4+6+8+12),则称该自然数为亏数;如果某自然数大于其所有真因子之和(例如8>1+2+4),则称该自然数为贏数;如果某自然数等于从1开始的若干个连续自然数之和(例如10=1+2+3+4)则称该自然数为三角形数。据此定义,自然数496是( )。供选择答案:A.亏数 B.赢数 C.完美数,非三角形数 D.完美数和三角形数
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子(即N的约数以及1,但不包括N)之和S,则称该数为“完美数”。例如6=1+2+3,28=1+2+4+7+14,所以6和28都是完美数。显然,6是第1个(即最小的)完美数。下面流程图的功能是求500以内所有的完美数。【流程图】
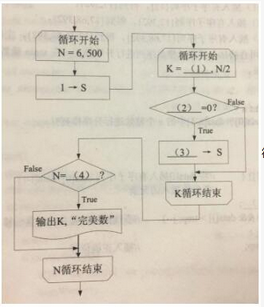
循环开始框中要注明:循环变量=初始值,终值[,步长],步长为1时可以缺省。如果某自然数小于其所有真因子之和(例如24<1+2+3+4+6+8+12),则称该自然数为亏数;如果某自然数大于其所有真因子之和(例如8>1+2+4),则称该自然数为贏数;如果某自然数等于从1开始的若干个连续自然数之和(例如10=1+2+3+4)则称该自然数为三角形数。据此定义,自然数496是( )。供选择答案:A.亏数 B.赢数 C.完美数,非三角形数 D.完美数和三角形数

循环开始框中要注明:循环变量=初始值,终值[,步长],步长为1时可以缺省。如果某自然数小于其所有真因子之和(例如24<1+2+3+4+6+8+12),则称该自然数为亏数;如果某自然数大于其所有真因子之和(例如8>1+2+4),则称该自然数为贏数;如果某自然数等于从1开始的若干个连续自然数之和(例如10=1+2+3+4)则称该自然数为三角形数。据此定义,自然数496是( )。供选择答案:A.亏数 B.赢数 C.完美数,非三角形数 D.完美数和三角形数
参考解析
解析:(1)2(2)N%K(3)S+K(4)S(5)D
【解析】
流程图的功能是求500以内所有的完美数,N的值范围是6~500,因此N是需要判断是否为完美数,首先需要求出N的所有真因子,然后再判断N和真因子之和是否相等,从流程图可以看出S是保存真因子和的变量,K是保存真因子的变量,因此K的初始值是2,终值是N/2,因此第(1)空处填写:2;判断K是否为N的真因子,即判断N%K(N除以K取余)是否为0,第(2)空填写:N%K;当K为N的真因子时,需要计算所有K的和,即S=S+K,第(3)空填写:S+K;最后判断N和S是否相等,第(4)空填写:S。496的真因子有:1、2、4、8、16、31、62、124、248,1+2+4+8+16+31+62+124+248=496;因此496是完美数,同时496=(1+2+3+4+……+30+31),因此496是完美数和三角形数。
【解析】
流程图的功能是求500以内所有的完美数,N的值范围是6~500,因此N是需要判断是否为完美数,首先需要求出N的所有真因子,然后再判断N和真因子之和是否相等,从流程图可以看出S是保存真因子和的变量,K是保存真因子的变量,因此K的初始值是2,终值是N/2,因此第(1)空处填写:2;判断K是否为N的真因子,即判断N%K(N除以K取余)是否为0,第(2)空填写:N%K;当K为N的真因子时,需要计算所有K的和,即S=S+K,第(3)空填写:S+K;最后判断N和S是否相等,第(4)空填写:S。496的真因子有:1、2、4、8、16、31、62、124、248,1+2+4+8+16+31+62+124+248=496;因此496是完美数,同时496=(1+2+3+4+……+30+31),因此496是完美数和三角形数。
相关考题:
下面的程序是10000以内的“相亲数”。所谓相亲数是指这样的一对数:甲数的约数之和等于乙数,而乙数的约数等于甲数,(例如220和284是一对相亲数)请在程序的每条横线处填写一条语句,使程序的功能完整。注意:请勿改动main()主方法和其他已有的语句内容,仅在横线处填入适当的语句。public class QinShu{public static void main(String args[ ]){for(int n=1;n<9999;n++){int s=divsum(n);if( )System.out.println(n+","+s);}}public static int divsum(int n){//该方法的功能是求一个数的所有约数int s=0;for(int i=1;____________________i++)if(____________________)s+=i;return s;}}
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)~(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。【流程图】
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。【说明】假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
阅读以下说明和流程图,将应填入(n)处的字句写在对应栏内。[说明]下面的流程图实现了正整数序列{K(1),K(2),…,K(n)}的重排,得到的新序列中,比K(1)小的数都在K(1)的左侧,比K(1)大的数都在K(1)的右侧。以n=6为例,序列{12,2,9,13,21,8}的重排过程为:{12,2,9,13,21,8}→{2,12,9,13,21,8}→{9,2,12,13,21,8}→{8,9,2,12,13,21}[流程图]
阅读以下说明和流程图,回答问题将解答填入对应栏内。[说明]已知递推数列:a(1)=1,a (2s)= a (s),a(2s+1)=a (s)+a (s+1)(s 为正整数)。试求该数列的第n项与前n项中哪些项最大?最大值为多少?算法分析:该数列序号分为奇数或偶数两种情况做不同递推,所得数列呈大小有规律的摆动。设置a数组,赋初值a (1)=1。根据递推式,在循环中分项序号s (2~n)为奇数或偶数作不同递推:每得一项 a (s),即与最大值max 作比较,如果a (s)>max,则max=a(i)。最后,在所有项中搜索最大项(因最大项可能多于一项),并打印最大值max。[问题]将流程图中的(1)~(5)处补充完整。注:流程图中(1)循环开始的说明按照“循环变量名:循环初值,循环终值,增量”格式描述。[流程图]
下面的程序是求9999以内的“完全数”。所谓完全数是指这样的自然数:它的各个约数(不包括该数自身)之和等于该数自身。如28=1+2+4+7+14就是一个完全数。请在程序的每条横线处填写一个语句,使程序的功能完整。注意:请勿改动main()主方法和其他已有的语句内容,仅在横线处填入适当的语句。public class QuanShu{public static void main(String args[]){for(int n=l;n<9999;n++)if(______________)System.out.println(n);}public static iht divsum(int n){//该方法功能是求一个数的所有约数int s=0;for(int i=l;i<n;i++)if(_________________)__________________return s;}}
阅读以下说明和流程图,回答问题1-2,将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法,实现了计算两正整数最大公约数的功能。给定正整数m和 n,假定m大于等于n,算法的主要步骤为:(1)以n除m并令r为所得的余数;(2)若r等于0,算法结束;n即为所求;(3)将n和r分别赋给m和n,返回步骤(1)。[流程图][问题1] 将流程图中的(1)~(4)处补充完整。[问题2] 若输入的m和n分别为27和21,则A中循环体被执行的次数是(5)。
阅读以下说明和C函数将应填入(n)处的字句写在答题纸的对应栏内【说明1】函数Counter(intn,intw[])的功能是计算整数n的二进制表示形式中的1个数同时用数组w记录该二进制数中1所在位置的权。例如十进制数22的二进制表示为10110.对于该二进制数,1的个数为3,在w[0]中存入2(即21)、w[1]中存入4(即22)w[2]存入16(即24)【C函数1】
阅读以下说明和流程图,回答问题将解答填入对应栏。[说明]下面的流程图,用来完成计算一组数组中的中值,其方法是:将数组中的一个值与其他值比较,并计算大于等于被比较数的数值的个数,以及小于等于被比较数的数值的个数,如果两数都大于n/2,则已经找到了中值,否则继续之前的步骤。注:流程中循环开始的说明按照“循环变量:循环初值,循环终值,增量”格式描述;[问题]将流程图的(1)~(5)处补充完整。
阅读以下说明和流程图,将应填入(n)处的字句写在对应栏内。[说明]下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”,其中句点表示结尾,空格之间连续的字母串称为单词。[流程图]
阅读以下说明和流程图,回答问题,并将解答填入对应栏内。【说明】求解约瑟夫环问题。算法分析:n个士兵围成一圈,给他们依次编号,班长指定从第w个士兵开始报数,报到第s个士兵出列,依次重复下去,直至所有士兵都出列。【流程图】【问题】将流程图中的(1)~(5)处补充完整。
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】设学生(学生数少于50人)某次考试的成绩按学号顺序逐行存放于某文件中,文件以单行句点“.”为结束符。下面的流程图用于读取该文件,并把全部成绩从高到低排序到数组B[50]中。【流程图】
阅读下列说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左到右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数X相等的数。如果找不到则输出false;只要找到一个(可能有多个)就输出True以及该元素的下标i和j(注意数组元素的下标从1开始)。 例如,在如下矩阵中查找整数8,则输出伟:True,4,1 2 4 6 9 4 5 9 10 6 7 10 12 8 9 11 13 流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数X进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.O(m*n) D,O(m+n)
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 下面流程图的功能是:在给定的一个整数序列中查找最长的连续递增子序列。设序列存放在数组 A[1:n](n2)中,要求寻找最长递增子序列 A[K: K+L-1] (即A[K]A[K+1]A[K+L-1])。流程图中,用 Kj 和Lj 分别表示动态子序列的起始下标和长度,最后输出最长递增子序列的起始下标 K 和长度 L。 例如,对于序列 A={1 ,2,4,4 ,5,6,8,9,4,5,8},将输出K=4, L=5。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为: 循环控制变量=初值,终值
阅读以下说明和流程图,填补流程图和问题中的空缺(1)~(5),将解答填入答题纸的对应栏内。 【说明】 设整型数组A[1:N]每个元素的值都是1到N之间的正整数。一般来说,其中会有一些元素的值是重复的,也有些数未出现在数组中。下面流程图的功能是查缺查重,即找出A[1:N]中所有缺的或重复的整数,并计算其出现的次数(出现次数为0时表示缺)。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1:N]加上的一个映射,并用数组C[1:N]记录各整数出现的次数,需输出所有缺少的或重复的数及其出现的次数。【流程图】【问题】 如果数组A[1:5]的元素分别为{3,2,5,5,1},则算法流程结束后输出结果为: (5) 。 输出格式为:缺少或重复的元素,次数(0表示缺少)
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有整数数组A[1:N](N1),其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大的和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(ji)的各元素之和S,并动态地记录其最大值M。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
?????? 阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)li=l,…,n}(n>1)}.其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)[j=l,…,m},而每个关键词K(j)出现的次数为NK(j).j=l,…,m。??????
试题一(共 15 分)阅读以下说明和流程图,填补流程图中的空缺(1)~(9) ,将解答填入答题纸的对应栏内。[说明]假设数组 A 中的各元素 A(1),A(2) ,…,A(M)已经按从小到大排序(M≥1) ;数组 B 中的各元素 B(1),B(2),…,B(N)也已经按从小到大排序(N≥1) 。执行下面的流程图后, 可以将数组 A 与数组 B 中所有的元素全都存入数组 C 中, 且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序) 。例如,设数组 A 中有元素:2,5,6,7,9;数组B 中有元素:2,3,4,7;则数组 C 中将有元素:2,2,3,4,5,6,7,7,9。[流程图]
阅读下列说明和流程图,填补流程图中的空缺(1)~(9),将解答填入答题纸的对应栏内。【说明】假设数组A中的各元素A⑴,A (2),…,A (M)已经按从小到大排序(M>1):数组B中的各元素B(1) , B (2) . B (N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序(注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素: 2,5,6,7,9;数组B中有元素: 2,3,4,7;则数组C中将有元素: 2,2,3,4,5,6,7,7,9.
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。[说明]本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n>1)},其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)|j=1,…,m},而每个关键词K(j)出现的次数为NK(j),j=1,…,m。[流程图]
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。1、【说明】 假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】如果n位数(n≧2)是回文数(从左到右读与从右到左读所得结果一致),且前半部分的数字递增(非减)、后半部分的数字将递减(非增),则称该数为拱形回文数。例如,12235753221 就是一个拱形回文数。显然,拱形回文数中不含数字0。下面的流程图用于判断给定的n位数(各位数字依次存放在数组的各个元素A[ i ]中,i =1,2,…,n)是不是拱形回文数。流程图中,变量T 动态地存放当前位之前一位的数字。当n 是奇数时,还需要特别注意中间一位数字的处理。【流程图】注1:“循环开始”框内给出的循环控制变量的初值、终值和增值(默认为1),格式为:循环款控制变量=初值,终值[ , 增值 ]注2:函数int(x)为取x的整数部分,即不超过x 的最大整数。
试题(15 分)阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏 内。【说明】设有整数数组 A[1:N](N>1),其元素有正有负。下面的流程图在该数组 中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标 K、元素 个数 L 以及最大的和值 M。例如,若数组元素依次为 3,-6,2,4,-2,3,-1,则输出 K=3,L=4,M=7。 该流程图中考察了 A[1:N]中所有从下标 i 到下标 j(j≥i)的各元素之和 S,并动态地记录其最大值 M。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为 1,格式为:循环控制变量=初值,终值
第一题 阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】对于大于1的正整数n,(x+1)n可展开为问题:1.1 【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。格式为:循环控制变量=初值,终值,递增值。
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间(a1