在圆中画一个与这个圆等半径、圆心角是60°的扇形,圆内其余部分的面积是这个扇形面积的多少:A4倍B5倍C6倍D8倍
在圆中画一个与这个圆等半径、圆心角是60°的扇形,圆内其余部分的面积是这个扇形面积的多少:
A4倍
B5倍
C6倍
D8倍
A4倍
B5倍
C6倍
D8倍
参考解析
解析:如图所示,扇形顶点与圆的圆心重合,此时,园内其余部分的面积是这个扇形面积的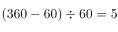

故正确答案为B。
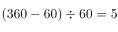

故正确答案为B。
相关考题:
单圆结构图的绘制步骤是( )。A.根据图纸大小,绘制一个圆形B.以各部分占总量的百分比乘360度,计算出各个扇形圆心角的度数C.根据各个扇形圆心角的度数计算扇形面积D.用量角器在圆中绘制各个扇形并填充不同的颜色或线纹E.标注各扇形所代表的项目名称
初中数学《圆的对称性》一、考题回顾二、考题解析【教学过程】(一)引入新课教师引导学生在纸上画两个大小相同的圆,然后将其剪下来,引导学生思考:将两个圆放在一起会怎么样?若将其中一个转动,两个圆是否还会重合?通过这两个问题让学生认识到圆是旋转的对称图形,进一步提问:对称中心是什么?进一步引导学生思考与圆的对称性有关的性质有哪些?引出课题。(二)探索新知对于导入中的问题,教师引导学生画两个完全相同的圆,然后将其中的一个圆剪下一个扇形AOB,引导学生将扇形AOB放在另外一个圆上,将顶点放在圆心上,画出扇形AOB,然后再引导学生将其旋转,再画出扇形A'OB',观察前后两个扇形,并思考:这两个扇形的中的圆心角、弦、弧有什么样的关系?预设:两个扇形是完全相同的。提问:扇形的大小由什么确定?预设:扇形的大小由圆心角确定。提问:能否用一句话说说上述的发现。预设:如果圆心角相等,那么它们所对的弧相等,所对的弦相等。进一步提问:在同一个圆呢?还是在两个圆中?若在两个圆中存在,这两个圆是什么关系。师生共同总结得出:在等圆和同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等。提问:能否说说上述结论中的条件和结论。预设:条件是在同圆或等圆中,圆心角相同,结论是:①所对的弧相等,②所对的弦相等。引导学生思考:如果互换条件和结论,那命题是否还正确?预设1:在同圆或等圆中,所对的弧相等,那么它们所对的圆心角相等,所对的弦也相等。预设2:在同圆或等圆中,所对的弦相等,那么它们所对的圆心角相等,所对的弧也相等。最后师生共同得出:在同圆或等圆中,已知三个量中的其中一个量相等,就可以得出另外两个量也相等。组织学生进行动手操作,折一折,说说圆是什么样的图形?进一步提问它的对称轴是什么?对称轴有多少条?最后师生共同得出:圆是对称图形,它的任意一条直径所在的直线都是它的对称轴。引导学生思考:怎样将圆平均分成2等分,4等分、8等分?进一步提问还可以将圆平均分成多少等分?最后师生共同得到:将圆沿直径对折平均分成2等分,再对折一次,平均成4等分,再对折就可以将圆平均分成8等分,再对折,就可以平均分成16等分了,再对折32等分等等。(三)课堂练习例1(四)小结作业提问:今天有什么收获?课后作业:思考当直径与弦垂直时,那所对的弧有什么关系?【板书设计】1.什么事对称图形?圆的对称轴有多少条??2.垂径定理是什么?
单选题喷灌喷头的喷洒方式有很多种,如全圆喷洒、扇形喷洒、矩形喷洒、带状喷洒等。在管道式喷灌系统中,主要采用(),而在田边路旁或房屋附近则使用()。()A扇形喷洒;全圆喷洒B带状喷洒;矩形喷洒C全圆喷洒;带状喷洒D全圆喷洒;扇形喷洒
判断题饼图利用圆形及圆内扇形面积来表示数值大小。( )A对B错