阅读以下说明和算法，完善算法并回答问题。【说明】假设以二维数组G[1..m，1..n)表示一幅图像各像素的颜色，则G[i，j]表示区域中点(i，j)处的颜色，颜色值为0～k的整数。下面的算法将指定点(i0，j0)所在的同色邻接区域的颜色置换为给定的颜色值。约定所有与点(i0，j0)同色的上、下、左、右可连通的点组成同色邻接区域。例如，一幅8×9像素的图像如图2-1所示。设用户指定点(3，5)，其颜色值为0，此时其上方(2，5)、下方(4，5)、右方(3，6)邻接点的颜色值都为0，因此这些点属于点(3，5)所在的同色邻接区域，再从上、下、左、右四个方向进行扩展，可得出该同色邻接区域的其他点(见图2-1中的阴影部分)。将上述同色区域的颜色替换为颜色值7所得的新图像如图2-2所示。【算法】输入：矩阵G，点的坐标(i0，j0)，新颜色值newcolor。输出：点(i0，j0)所在同色邻接区域的颜色置换为newcolor之后的矩阵G。算法步骤(为规范算法，规定该算法只在第七步后结束)如下。第一步：若点(i0，j0)的颜色值与新颜色值newcolor相同，则(1)；第二步：点(i0，j0)的颜色值→oldcolon创建栈S，并将点坐标(i0，j0)入栈；第三步；若(2)，则转第七步；第四步；栈顶元素出栈→(x,y)，并(3)；第五步；1)若点(x，y-1)在图像中且G[x，y-1]等于oldcolor，则(x,y-1)入栈S；2)若点(x，y+1)在图像中且GIx，y+1]等于oldeolor，则(x，y+1)入栈S；3)若点(x-1，y)在图像中且G[x-1，y)等于oldcolor，则(x-1，y)入栈S；4)若点(x+1，y)在图像中且G[x+1，y)等于oldcolor，则(x+1，y)入栈S；第六步：转(4)；第七步：算法结束。【问题】是否可以将算法中的栈换成队列?回答；(5) 。
阅读以下说明和算法，完善算法并回答问题。
【说明】
假设以二维数组G[1..m，1..n)表示一幅图像各像素的颜色，则G[i，j]表示区域中点(i，j)处的颜色，颜色值为0～k的整数。
下面的算法将指定点(i0，j0)所在的同色邻接区域的颜色置换为给定的颜色值。约定所有与点(i0，j0)同色的上、下、左、右可连通的点组成同色邻接区域。
例如，一幅8×9像素的图像如图2-1所示。设用户指定点(3，5)，其颜色值为0，此时其上方(2，5)、下方(4，5)、右方(3，6)邻接点的颜色值都为0，因此这些点属于点(3，5)所在的同色邻接区域，再从上、下、左、右四个方向进行扩展，可得出该同色邻接区域的其他点(见图2-1中的阴影部分)。将上述同色区域的颜色替换为颜色值7所得的新图像如图2-2所示。
【算法】
输入：矩阵G，点的坐标(i0，j0)，新颜色值newcolor。
输出：点(i0，j0)所在同色邻接区域的颜色置换为newcolor之后的矩阵G。
算法步骤(为规范算法，规定该算法只在第七步后结束)如下。
第一步：若点(i0，j0)的颜色值与新颜色值newcolor相同，则(1)；
第二步：点(i0，j0)的颜色值→oldcolon创建栈S，并将点坐标(i0，j0)入栈；
第三步；若(2)，则转第七步；
第四步；栈顶元素出栈→(x,y)，并(3)；
第五步；1)若点(x，y-1)在图像中且G[x，y-1]等于oldcolor，则(x,y-1)入栈S；
2)若点(x，y+1)在图像中且GIx，y+1]等于oldeolor，则(x，y+1)入栈S；
3)若点(x-1，y)在图像中且G[x-1，y)等于oldcolor，则(x-1，y)入栈S；
4)若点(x+1，y)在图像中且G[x+1，y)等于oldcolor，则(x+1，y)入栈S；
第六步：转(4)；
第七步：算法结束。
【问题】
是否可以将算法中的栈换成队列?回答；(5) 。
相关考题：
阅读下列程序说明和C代码，把应填入其中n处的字句写在答卷的对应栏内。【说明】程序利用选择排序算法对数组a中的N个整数按照从小到大的顺序排列，并将排序结果显示出来。【程序】define N 10main(){void (1)；int i，a[N]；for(i=0；i＜10，i++) /*输入*/scanf(“%d”，a[i])；(2)；for(i=0；i＜N，i++) /*输出*/printf(“%3d”，a[i])；}void selectSon(int x[]，int n){int i，j，k，t；for(int i=0； (3)；i++){k=i；for(j=i+1；j＜n；j++)if (4) k=j；if (5){t=x[i]；x[i]=x[k]；x[k] =t；}}}
设二维数组A[1..m,1..n](即m行n列)按行存储在数组B[1..m*n]中,则二维数组元素A[i,j]在一维数组B中的下标为()。 A.(i-1)*n+jB、(i-1)*n+j-1C.i*(j-1)D、j*m+i-1
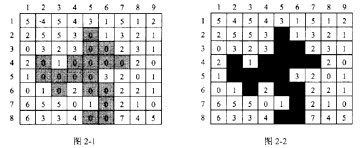
阅读以下说明和算法，完善算法并回答问题，将解答写在对应栏内。[说明]假设以二维数组G[1..m,1..n]表示一幅图像各像素的颜色，则G[i,j]表示区域中点(i,j]处的颜色，颜色值为0到k的整数。下面的算法将指定点(i0,j0)所在的同色邻接区域的颜色置换为给定的颜色值。约定所有与点(i0,j0)同色的上、下、左、右可连通的点组成同色邻接区域。例如，一幅8×9像素的图像如图1-1所示。设用户指定点(3,5)，其颜色值为0，此时其上方(2,5)、下方(4,5)、右方(3,6)邻接点的颜色值都为0，因此这些点属于点(3,5)所在的同色邻接区域，再从上、下、左、右四个方向进行扩展，可得出该同色邻接区域的其他点(见图1-1中的阴影部分)。将上述同色区域的颜色替换为颜色值7所得的新图像如图1-2所示。[算法]输入：矩阵G，点的坐标(i0,j0)，新颜色值newcolor。输出：点(i0,j0)所在同色邻接区域的颜色置换为newcolor之后的矩阵G。算法步骤(为规范算法，规定该算法只在第七步后结束)：第一步：若点(i0,j0)的颜色值与新颜色值newcolor相同，则(1)；第二步：点(i0,j0)的颜色值→oldcolor；创建栈S，并将点坐标(i0,j0)入栈；第三步：若(2)，则转第七步；第四步：栈顶元素出栈→(x,y)，并(3)；第五步：1) 若点(x,y-1)在图像中且G[x,y-1]等于oldcolor,则(x,y-1)入栈S；2) 若点(x,y+1)在图像中且G[x,y+1]等于oldcolor,则(x,y+1)入栈S；3) 若点(x-1,y)在图像中且G[x-1,y]等于oldcolor,则(x-1,y)入栈S；4) 若点(x+1,y)在图像中且G[x+1,y)等于oldcolor,则(x+1,y)入栈S：第六步：转(4)；第七步：算法结束。[问题]是否可以将算法中的栈换成队列?回答：(5)。
●试题一阅读以下算法说明和流程图，回答问题1和问题2。【算法说明】下面是一段插入排序的程序，将R[k+1]插入到R[1…k]的适当位置。R[0]=R[k+1]；j=k；while (R[j]R[0]){R[j+1]=R[j]；j--；}R[j+1]=R[0]；【流程图】【测试用例设计】(while循环次数为0、1、2次)【问题1】指出算法的流程图中 (1) ～ (3) 处的内容。【问题2】指出测试用例设计中 (4) ～ (9) 处的内容。
试题一（共 15分）阅读以下说明和算法，完善算法并回答问题，将解答写在答题纸的对应栏内。[说明]假设以二维数组G[1..m,1..n]表示一幅图像各像素的颜色，则G[i,j]表示区域中点(i,j)处的颜色，颜色值为0到k 的整数。下面的算法将指定点(i0,j0)所在的同色邻接区域的颜色置换为给定的颜色值。约定所有与点(i0,j0)同的上、下、左、右可连通的点组成同色邻接区域。例如，一幅8×9 像素的图像如图1-1 所示。设用户指定点(3,5)，其颜色值为0，此时其上方(2,5)、下方 (4,5)、右方(3,6)邻接点的颜色值都为0，因此这些点属于点(3,5)所在的同色邻接区域，再从上、下、左、右四个方向进行扩展，可得出该同色邻接区域的其他点（见图1-1 中的阴影部分）。将上述同色区域的颜色替换为颜色值7所得的新图像如图1-2 所示。[算法]输入：矩阵 G，点的坐标(i0,j0)，新颜色值newcolor。输出：点(i0,j0)所在同色邻接区域的颜色置换为newcolor之后的矩阵G。算法步骤(为规范算法，规定该算法只在第七步后结束)：第一步：若点(i0,j0)的颜色值与新颜色值newcolor相同,则(1) ；第二步：点(i0,j0)的颜色值→oldcolor；创建栈S，并将点坐标(i0,j0)入栈；第三步：若 (2) ，则转第七步；第四步：栈顶元素出栈→(x,y)，并(3) ；第五步：1) 若点(x,y-1)在图像中且G[x,y-1]等于oldcolor，则(x,y-1)入栈S；2) 若点(x,y+1)在图像中且G[x,y+1]等于oldcolor，则(x,y+1)入栈S；3) 若点(x-1,y)在图像中且G[x-1,y]等于oldcolor，则(x-1,y)入栈S；4) 若点(x+1,y)在图像中且G[x+1,y]等于oldcolor，则(x+1,y)入栈S；第六步：转 (4) ；第七步：算法结束。[问题]是否可以将算法中的栈换成队列？回答： (5) 。
阅读下列说明和C代码，回答问题，将解答填入答题纸的对应栏内。【说明】计算一个整数数组a的最长递增子序列长度的方法描述如下：假设数组a的长度为n，用数组b的元素b[i]记录以a[i](0≤i＜n)为结尾元素的最长递增子序列的长度为 ；其中b[i]满足最优子结构，可递归定义为：【C代码】下面是算法的C语言实现。（1）常量和变量说明a：长度为n的整数数组，待求其最长递增子序列b：长度为n的数组，b[i]记录以a[i](0≤ilen：最长递增子序列的长度i, j：循环变量temp：临时变量（2）C程序#include int maxL(int*b, int n) {int i, temp=0;for(i=0; itemp) temp=b[i]; } return temp;}int main() { int n,a[100], b[100], i, j, len; scanf("%d", for(i=0;i【问题1】（8分）根据说明和C代码，填充C代码中的空（1）～（4）。【问题2】（4分） 根据说明和C代码，算法采用了 （5） 设计策略，时间复杂度为 （6） （用O符号表示）。【问题3】（5分） 已知数组a={3，10，5，15，6，8}，据说明和C代码，给出数组b的元素值。
阅读下列说明和C代码，回答下列问题。[说明] 计算一个整数数组a的最长递增子序列长度的方法描述如下： 假设数组a的长度为n，用数组b的元素b[i]记录以a[i](0≤i＜n”)为结尾元素的最长递增子序列的长度为其中b[i]满足最优子结构，可递归定义为： [C代码] 下面是算法的C语言实现。 10常量和变量说明 a:长度为n的整数数组，待求其最长递增子序列 b:长度为n的数组，b[i]记录以a[i](0≤i＜n”)为结尾元素的最长递增子序列的长度，其中0≤i＜n len:最长递增子序列的长度 i,j:循环变量 temp:临时变量 11C程序 # jnclude＜stdio,h＞ mtmaxL(int*b,mt n) { mt I, temp=0 for(i=0; i＜n; i++) { (b[i]＞temp) temp=b[i] return temp; int main12 { int n,a[100],b[100],i,j,len; scanf(" % d", for(i=0;i＜n;i++) { scanf("% d", ___1___: for(i=1;i＜n;i++) { for(j=0,len=0;___2___;j++){ if( ___3___ } Printf("len:% d\n",maxL(b,n)) Primtf("\n") }1~4、 根据说明和C代码，填充C代码中的空______～______。5、 根据说明和C代码，算法采用了______设计策略，时间复杂度为______(用O符号表示)6、 已知数组a={3，10，5，15，6，8}，据说明和C代码，给出数组b的元素值。
1、 以下算法是某个重要算法的一个版本，阅读后请求出该算法的时间效率，同时分析该算法有哪些重要缺陷，该如何弥补。 算法 GE（A[0..n-1,0..n-1]) for iß0 to n-2 do for jßi+1 to n-1 do for kßn downto i do A[j,k]ßA[j,k]-A[I,k]*A[j,i]/A[I,i]
2、以下算法是某个重要算法的一个版本，阅读后请求出该算法的时间效率，同时分析该算法有哪些重要缺陷，该如何弥补。 算法 GE（A[0..n-1,0..n-1]) for iß0 to n-2 do for jßi+1 to n-1 do for kßn downto i do A[j,k]ßA[j,k]-A[I,k]*A[j,i]/A[I,i]