检查五位同学统计学原理的学习时间与学习成绩情况,调查资料整理如下:要求:(1)计算学习时数与学习成绩之间的相关系数,并说明两变量相关的方向和程度(2)建立学习成绩倚学习时数的直线回归方程
检查五位同学统计学原理的学习时间与学习成绩情况,调查资料整理如下:
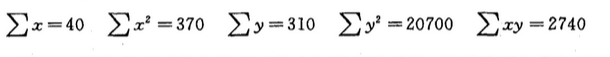
要求:(1)计算学习时数与学习成绩之间的相关系数,并说明两变量相关的方向和程度
(2)建立学习成绩倚学习时数的直线回归方程
相关考题:
某班 40 名学生,按某课程的学习时数每 8 人为一组进行分组,其对应的学习成绩如下表:试根据上述资料建立学习成绩(y)倚学习时间(x)的直线回归方程。 (要求列表计算所需数据资料,写出公式和计算过程,结果保留两位小数。)
一项调查显示,某班参加挑战杯比赛的同学,与那些未参加此项比赛的同学相比,学习成绩一直保持较高的水平。此项调查得出结论:挑战杯比赛通过开拓学生的视野,增加学生的学习兴趣,激发学生的创造潜力,有效地提高了学生的学习成绩。 以下哪项如果为真,最能加强上述调查结论的说服力?( ) A.没有参加挑战杯比赛的同学如果通过其他活动开拓视野,也能获得好成绩 B.整天在教室内读书而不参加课外科技活动的学生,他们的视野、学习兴趣和创造力可能会受到影响 C.没有参加挑战杯比赛的同学大都学习很努力 D.参加挑战杯比赛并不以学习成绩好为条件
调查五位学生《统计学原理》的学习时间与成绩(5分制)情况,调查资料如下表所示: 学习时间(小时) 学习成绩(分) 1 3 1 4 2 3 2 5 4 5 根据资料:(1)计算学习时间与学习成绩之间的相关系数。 (2)建立学习成绩倚学习时间的直线回归方程。 (3)若某同学学习时间为3小时,试估计其成绩。
在计算机支持的协作学习中,A同学最终形成的答案比B同学要“准确”,就可以说明A同学的协作学习成绩比B同学要好。