如果F实现一个程序,输入变量x1和x2的边界、区间分别为:a≤x1≤d,区间为[a,b],[b,c],[c,d];e≤x2≤g,区间为[e,f],[f,g];则下列_ d_图可表示为强健壮等价类测试用例。A.AB.BC.CD.D
如果F实现一个程序,输入变量x1和x2的边界、区间分别为:a≤x1≤d,区间为[a,b],[b,c],[c,d];e≤x2≤g,区间为[e,f],[f,g];则下列_ d_图可表示为强健壮等价类测试用例。

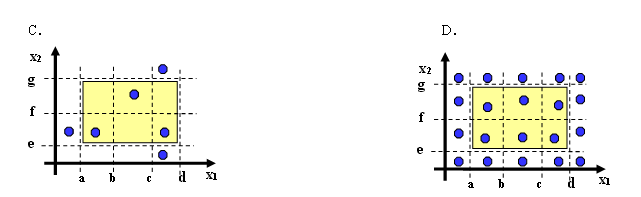
A.A
B.B
C.C
D.D
相关考题:
已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。 A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)
6、x(t)为x1(t)和x2(t)相乘,x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则x(t)的傅里叶变换为()。A.X1(f)和X2(f)的卷积B.X1(f)乘以X2(f)C.X1(f)+X2(f)D.不确定
若随机变量的分布函数为F(x),下列一定正确的是:A.P(X=x)=F(x)-F(x-0)B.P(x1<X≤x2)=F(x2)-F(x1)C.P(x1≤X≤x2)=F(x2)-F(x1)D.P(x1≤X<x2)=F(x2)-F(x1)
函数 f(x) 在区间 [a,b] 上连续,在 (a,b) 内可导,a < x1 < x2 < b, 则至少存在一点 ξ, 使得下列等式必然成立的个数 1.f(b) − f(a) = f′(ξ)(b − a), ξ ∈ (a, b). 2.f(x2) − f(x1) = f′(ξ)(x2 − x1), ξ ∈ (a, b). 3.f(b) − f(a) = f′(ξ)(b − a), ξ ∈ (x1, x2). 4.f(x2) − f(x1) = f′(ξ)(x2 − x1), ξ ∈ (x1, x2).A.1 个.B.2 个.C.3 个.D.4 个.
非线性模型中,当其他自变量保持不变,X1 变化△X1,因变量的期望值的变化量为:A.△Y = f(X1 + X1, X2,... Xk).B.△Y = f(X1 + △X1, X2 + △X2,..., Xk+ △Xk)- f(X1, X2,...Xk).C.△Y = f(X1 + △X1, X2,..., Xk)- f(X1, X2,...Xk).D.△Y = f(X1 + X1, X2,..., Xk)- f(X1, X2,...Xk).
30、x(t)为x1(t)和x2(t)相乘,x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则x(t)的傅里叶变换为()。A.X1(f)和X2(f)的卷积B.X1(f)乘以X2(f)C.X1(f)+X2(f)D.不确定
15、x(t)为x1(t)和x2(t)相乘,x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则x(t)的傅里叶变换为()。A.X1(f)和X2(f)的卷积B.X1(f)乘以X2(f)C.X1(f)+X2(f)D.不确定
f(x)在区间[x1,x3]上为单峰函数,x2为区间中的一点,x4为利用二次插值法求得的近似极值点,若x4-x2<0,且f(x4)≥f(x2),则新的搜索区间为()。A.[x1,x4]B.[x2,x3]C.[x1,x2]D.[x4,x3]