有理数域Q上的代数运算是( ).A.B.C.D.
有理数域Q上的代数运算是( ).
A.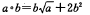
B.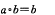
C.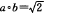
D.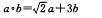
相关考题:
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的,∈S,有*=,则S 设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的<a,b>,<x,y>∈S,有<a,b>*<x,y>=<ax,ay+b>,则S中关于运算*的单位元为______。A.<1,0>B.<0,1>C.<1,1>D.<0,0>A.B.C.D.
下列说法正确的有()。A.实数域关于数的加法和乘法构成自身上的线性空间B.有理数域关于数的加法和乘法构成实数上的线性空间C.复数域关于数的加法和乘法构成有理数域上的线性空间D.实数域关于数的加法和乘法构成复数域上的线性空间
有理数域对于本身的加法与乘法运算作成实数域上的线性空间。