作直线相关分析时,当,n=10,r=0.8531,α=0.05(双侧),查相关系数界值表r=0.872,r=0.847,r=0.805,得P值范围为A.0.001<P<0.002B.P<0.001C.0.0005<P<0.001D.P<0.0005E.0.002<P<0.005
作直线相关分析时,当,n=10,r=0.8531,α=0.05(双侧),查相关系数界值表r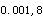 =0.872,r
=0.872,r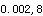 =0.847,r
=0.847,r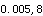 =0.805,得P值范围为
=0.805,得P值范围为
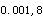 =0.872,r
=0.872,r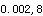 =0.847,r
=0.847,r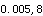 =0.805,得P值范围为
=0.805,得P值范围为A.0.001<P<0.002
B.P<0.001
C.0.0005<P<0.001
D.P<0.0005
E.0.002<P<0.005
B.P<0.001
C.0.0005<P<0.001
D.P<0.0005
E.0.002<P<0.005
参考解析
解析:作直线相关分析时,当n=10,r=0.8531,α=0.05(双侧)查相关系数界值表r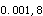 =0.872,r
=0.872,r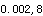 =0.847,r
=0.847,r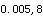 =0.805,得P值范围为<0.001<P<0.002,答案A正确。在相同的自由度上,r绝对值越大,P越小,反之,r绝对值越小,P越大。题中r<r
=0.805,得P值范围为<0.001<P<0.002,答案A正确。在相同的自由度上,r绝对值越大,P越小,反之,r绝对值越小,P越大。题中r<r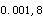 P>0.001r>r
P>0.001r>r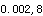 P<0.002连起来写即0.001<P<0.002。
P<0.002连起来写即0.001<P<0.002。
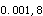 =0.872,r
=0.872,r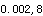 =0.847,r
=0.847,r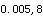 =0.805,得P值范围为<0.001<P<0.002,答案A正确。在相同的自由度上,r绝对值越大,P越小,反之,r绝对值越小,P越大。题中r<r
=0.805,得P值范围为<0.001<P<0.002,答案A正确。在相同的自由度上,r绝对值越大,P越小,反之,r绝对值越小,P越大。题中r<r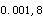 P>0.001r>r
P>0.001r>r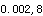 P<0.002连起来写即0.001<P<0.002。
P<0.002连起来写即0.001<P<0.002。
相关考题:
作直线相关分析时,当n=10,r=0.8531,α=0.05(双侧),查相关系数界值表r0.001,8=0.872,r0.002,8=0.847,r0.005,8=0.805,得P值范围为A、0.001B、PC、0.0005D、PE、0.002
两个变量(x,y),其观测值为(xi,yi),i=1,2,…,n。当相关系数的绝对值|r|大于某个临界值时,就认为它们之间存在一定的线性相关关系。若给定显著水平α,则临界值为( )。A.r1-α(n-1)B.r1-α/2(n-1)C.r1-α(n-2)D.r1-α/2(n-2)
某研究欲比较单纯肥胖者(n1=8)与正常人(n2=10)血浆总皮质醇是否有差异,采用Wilcoxon两样本比较的秩和检验。计算得单纯肥胖者的秩和T1=74.5,正常人的秩和T2=96.5,查两样本比较的T界值表:当双侧a=0.10时,T界值范围为56~96;当双侧a=0.05时,T界值范围为53~99;当双侧a=0.01时,T界值范围为47~105。则P为A.P0.10B.0.05P0.10C.P=0.05D.0.01P0.05E.P0.01
为调查研究某地l0个乡的肝癌死亡率与某种物质相对含量是否呈等级相关,取a=0.05,已算得r1=0.682,查r5相关系数界值表,双侧检验,n=10时,P=0.05的界值为0.648,n=9时,P=0.05的界值为0.700,则A.P0.05,可认为其相关B.P0.05,不能认为其相关C.P<0.05,可认为其相关D.P<0.05,不能认为其相关E.不拒绝H。,还不能认为其相关
在秩相关的分析中,下列描述正确的是A.它更适用于服从双变量正态分布的资料B.r界值表的自由度为ν=n-2C.总体分布类型未知的资料宜计算rD.查r界值表时,计算的统计量|r|越小,所对应的P越小E.r≤1
为调查研究某地10个乡的肝癌死亡率与某种物质相对含量是否呈等级相关,取α=0.05,已算得r=0.682,查r相关系数界值表,双侧检验,n=10时,P=0.05的界值为0.648,n=9时,P=0.05的界值为0.700,则A.P>0.05,可认为其相关B.P>0.05,不能认为其相关C.P<0.05,可认为其相关D.P<0.05,不能认为其相关E.不拒绝H,还不能认为其相关
实验室对30块混凝土试件进行强度试验,分别测定了其抗压强度R和回弹值N,现建立了R—N的线性回归方程。经计算LXX=632.47,LXY=998.46,LYY=1788.36,相关系数临界值r(0.05,28)=0.361,检验R—N的相关性()。A、r=0.4733,r>0.361,R—N之间线性相关B、r=0.9388,r>0.361,R—N之间线性相关C、r=0.4733,0.361<r,R—N之间无线性相关D、r=0.9388,0.361<r,R—N之间无线性相关
作直线相关分析时,当,n=10,r=0.8531,α=0.05(双侧),查相关系数界值表r0.001,8=0.872,r0.002,8=0.847,r0.005,8=0.805,得P值范围为()A、0.001B、P0.001C、0.0005D、P0.0005E、0.002
某研究欲比较单纯肥胖者(n1=8)与正常人(n2=10)血浆总皮质醇是否有差异,采用Wilcoxon两样本比较的秩和检验。计算得单纯肥胖者的秩和T1=74.5,正常人的秩和T2=96.5,查两样本比较的T界值表:当双侧a=0.10时,T界值范围为56~96;当双侧a=0.05时,T界值范围为53~99;当双侧a=0.01时,T界值范围为47~105。则P值为()A、P0.10B、0.05C、P=0.05D、0.01E、P0.01
实验室对30块混凝土试件进行强度试验,分别测定了其抗压强度R和回弹值N,现建立了R-N的线性回归方程,经计算Lxx=632.47;Lxy=998.46;Lyy=1788.36,相关系数的临界值r(0.05,28)=0.361,检验R-N是相关性()A、r=0.4733,r0.361;R-N之间线性相关B、r=0.9388,r0.361;R-N之间线性相关C、r=0.4733,0.361
实验室对30块混凝土试件进行强度试验,分别测定了其抗压强度R和回弹值N,现建立了R-N的线性回归方程,经计算Lxx=632.47Lxy=998.46Lyy=1788.36,相关系数的临界值r(0.05,28)=0.361,检验R-N是相关性()A、r=0.4733,r0.361,R-N之间线性相关B、r=0.9388,r0.361R-N之间线性相关C、r=0.4733,0.361D、r=0.9388,0.361
单选题作直线相关分析时,当,n=10,r=0.8531,α=0.05(双侧),查相关系数界值表r0.001,8=0.872,r0.002,8=0.847,r0.005,8=0.805,得P值范围为()A0.001BP0.001C0.0005DP0.0005E0.002
单选题实验室对30块混凝土试件进行强度试验,分别测定了其抗压强度R和回弹值N,现建立了R—N的线性回归方程。经计算LXX=632.47,LXY=998.46,LYY=1788.36,相关系数临界值r(0.05,28)=0.361,检验R—N的相关性()。Ar=0.4733,r>0.361,R—N之间线性相关Br=0.9388,r>0.361,R—N之间线性相关Cr=0.4733,0.361<r,R—N之间无线性相关Dr=0.9388,0.361<r,R—N之间无线性相关
单选题实验室对30块混凝土试件进行强度试验,分别测定了其抗压强度R和回弹值N,现建立了R-N的线性回归方程,经计算Lxx=632.47;Lxy=998.46;Lyy=1788.36,相关系数的临界值r(0.05,28)=0.361,检验R-N是相关性()Ar=0.4733,r0.361;R-N之间线性相关Br=0.9388,r0.361;R-N之间线性相关Cr=0.4733,0.361