高中数学《直线与平面垂直的判定》一、考题回顾二、考题解析【教学过程】(一)引入新课直接阐述生活中有很多直线和平面垂直的现象,直接引出本节课的学习内容《直线与平面垂直的判定》。(二)探索新知1.直线与平面垂直的概念图片展示旗杆与地面、大桥的桥柱与水面的图片。提问:通过对这些现象的观察,说一说旗杆与地面、大桥的桥柱与水面给大家的直观感受是什么?再说一说生活中还有哪些直线与平面垂直的现象?预设:图片中旗杆与地面、大桥的桥柱与水面给人垂直的现象。教室中的桌腿和地面、两面墙相交的直线与地面……展示将旗杆与地面抽象成数学图形。1.判断直线与平面垂直的方法有哪些?2.直线与平面平行的判定定理是什么?如何推导出来的?
高中数学《直线与平面垂直的判定》
一、考题回顾

二、考题解析
【教学过程】
(一)引入新课
直接阐述生活中有很多直线和平面垂直的现象,直接引出本节课的学习内容《直线与平面垂直的判定》。
(二)探索新知
1.直线与平面垂直的概念
图片展示旗杆与地面、大桥的桥柱与水面的图片。
提问:通过对这些现象的观察,说一说旗杆与地面、大桥的桥柱与水面给大家的直观感受是什么?再说一说生活中还有哪些直线与平面垂直的现象?
预设:图片中旗杆与地面、大桥的桥柱与水面给人垂直的现象。
教室中的桌腿和地面、两面墙相交的直线与地面……
展示将旗杆与地面抽象成数学图形。


1.判断直线与平面垂直的方法有哪些?
2.直线与平面平行的判定定理是什么?如何推导出来的?
一、考题回顾

二、考题解析
【教学过程】
(一)引入新课
直接阐述生活中有很多直线和平面垂直的现象,直接引出本节课的学习内容《直线与平面垂直的判定》。
(二)探索新知
1.直线与平面垂直的概念
图片展示旗杆与地面、大桥的桥柱与水面的图片。
提问:通过对这些现象的观察,说一说旗杆与地面、大桥的桥柱与水面给大家的直观感受是什么?再说一说生活中还有哪些直线与平面垂直的现象?
预设:图片中旗杆与地面、大桥的桥柱与水面给人垂直的现象。
教室中的桌腿和地面、两面墙相交的直线与地面……
展示将旗杆与地面抽象成数学图形。


1.判断直线与平面垂直的方法有哪些?
2.直线与平面平行的判定定理是什么?如何推导出来的?
参考解析
解析:1.
(1)定义法。
(2)利用判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
2.
定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
推导:在翻书过程中,通过对书本的边缘所在直线与桌面所在的平面之间的关系,探究得到直线与平面平行判定定理的初步认识;
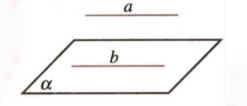
再利用直接探究如下图形,探究得出判定定理。
(1)定义法。
(2)利用判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
2.
定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
推导:在翻书过程中,通过对书本的边缘所在直线与桌面所在的平面之间的关系,探究得到直线与平面平行判定定理的初步认识;
再利用直接探究如下图形,探究得出判定定理。

相关考题:
一、考题回顾题目来源:1月6日下午陕西省西安市面试考题试讲题目:高中数学《直线与平面平行的判定定理》3基本要求:(1) 要有板书;(2) 试讲十分钟左右;(3) 条理清晰,重点突出;(4)学生掌握直线与平面平行的判定定理。答辩题目1简单随机抽样的方法有哪些,为什么这些抽样方法统称为简单随机抽样?2 课堂练习设置的原则是什么?
阅读下列三位教师关于“直线与平面垂直的判定”的教学片段。教师甲的引入:教师甲:同学们,空间直线与平面有哪几种位置关系?学生边演示边叙述,得到直线与平面的三种位置关系。教师:直线在平面内.直线与平面的平行已研究过,直线与平面相交成为今天要研究的问题。在日常生活中,你见过哪些情景可以抽象成直线与平面相交?举例说明。学生:日光灯的掉线与天花板相交;房子的柱子与天花板相交:插在碗里的筷子与平的碗底相交。教师:想象力丰富。生活中确实有很多例子。例如,墙角与地面(图片展示),小区的建筑,竹竿与水平面以及古诗词中的自然景观“大漠孤烟直”,“一行白鹭上青天”。在直线与平面相交的模型中,你认为哪种相交最特殊?学生:直线与平面垂直。教师:今天我们就研究这种关系。(板书课题)教师乙的引入:教师:(用PPT呈现龙卷风图片)同学们刚进教室看到这样的壮丽图片,联想起“大漠孤烟直”的美景,大家欣赏完之后是否想到立体几何中什么与什么的关系?学生:线面垂直。教师:很好,那生活中有没有这样的例子?学生:看电视时,视线与画面;电线杆与地面垂直。教师:这样的例子很多。比如,大桥桥柱与水面。正因为生活中有很多线与面垂直关系,所以几何中有必要对此进行研究。这堂课就学习直线与平面垂直。(板书课题)教师丙的引入:教师:前面我们研究了直线与平面平行的判定与性质,今天我们要研究直线与平面的其他位置关系。(展示天安门广场上的国旗与旗杆)先请大家看一幅图:天安门广场的红旗迎风飘扬。再看另一幅图:一桥飞架南北,天堑变通途。请大家回答下面的闩题。问题:请同学们观察图片,说出旗杆与地面,大桥桥柱与水平面是什么位置关系?学生:垂直。教师:从教学的角度看,就是什么与什么垂直。学生:线与面。教师:你还能举出一些类似的例子吗?想一想。(同时出示课题)学生1:箱的边缘与地面。学生2:立竿见影,竿与地面垂直。教师又展示跨栏跳高架的图片,说明跨栏的支架与地面,跳高架立竿与地面是垂直关系,请大家参照旗杆与地面这种关系画出相应的几何图形。学生画图.教师在黑板上画出图。教师:为什么画成这样呢?这样直观性强,将直线画得与表示平面的平行四边形的一边垂直。教师:接着前面的内容的学习,下面我们要学习直线与平面垂直的定义、判定与性质。问题:(1)三种引入方式各有什么特点?(10分)(2)在(1)的基础上,给出你对课题引入的观点。(10分)
案例:阅读下列三位教师关于“直线与平面垂直的判定”的教学片段。 教师甲的引入: 教师甲:同学们,空间直线与平面有哪几种位置关系 学生边演示边叙述,得到直线与平面的三种位置关系。 教师:直线在平面内,直线与平面的平行已研究过.直线与平面相交成为今天要研究的问题。在日常生活中,你见过哪些情景可以抽象成直线与平面相交 举例说明。 学生:日光灯的掉线与天花板相交;房子柱子与天花板相交:插在碗里的筷子与平的碗底相交。 教师:想象力丰富。生活中确实有很多例子。例如,墙角与地面(图片展示),小区的建筑,竹竿与水平面以及古诗词中的自然景观“大漠孤烟直”,“一行白鹭上青天”。在直线与平面相交的模型中,你认为哪种相交最特殊 学生:直线与平面垂直。 教师:今天我们就研究这种关系。(板书课题) 教师乙的引入: 教师:(用PPT呈现龙卷风图片)同学们刚进教室看到这样的壮丽图片,联想起“大漠孤烟直”的美景,大家欣赏完之后是否想到立体几何中什么与什么的关系 学生:线面垂直。 教师:很好。那生活中有没有这样的例子 学生:看电视时,视线与画面;电线杆与地面垂直。 教师:这样的例子很多。比如,大桥桥柱与水面。正因为生活中有很多线与面垂直关系.所以几何中有必要对此进行研究。这堂课就学习直线与平面垂直。(板书课题) 教师丙的引入: 教师:前面我们研究了直线与平面平行的判定与性质.今天我们要研究直线与平面的其他位置关系。(展示天安门广场上的国旗与旗杆)先请大家看一幅图:天安门广场的红旗迎风飘扬。再看另一幅图:一桥飞架南北,天堑变通途。请大家回答下面的问题。 问题:请同学们观察图片,说出旗杆与地面,大桥桥柱与水平面是什么位置关系 学生:垂直。 教师:从教学的角度看,就是什么与什么垂直。 学生:线与面。 教师:你还能举出一些类似的例子吗 想一想。(同时出示课题) 学生1:箱的边缘与地面。 学生2:立竿见影,竿与地面垂直。 教师又展示跨栏跳高架的图片,说明跨栏的支架与地面,跳高架立竿与地面是垂直关系,请大家参照旗杆与地面这种关系画出相应的几何图形。 学生画图,教师在黑板上画出图。 教师:为什么画成这样呢 这样直观性强,将直线画得与表示平面的平行四边形的一边垂直。 教师:接着前面的内容的学习,下面我们要学习直线与平面垂直的定义、判定与性质。 问题: (1)三种引入方式各有什么特点 (2)在(1)的基础上,给出你对课题引入的观点。
单选题下列四个条件中,能使结论“直线a⊥平面α”成立的是( ).A直线a与平面α内的两条直线垂直B直线a与平面α内的无数条直线垂直C直线a在α的一个垂直平面内D直线a与平面α的一个平行平面垂直
单选题下列命题中正确的是( ).A两平行线之一平行于一个平面,则另一条直线也平行于这个平面B两平行线之一垂直于一个平面,则另一条直线也垂直于这个平面C两直线与同一平面平行,则两直线平行D两直线与同一平面成等角,则两直线平行
单选题下列四个命题中,错误的个数是( ).①如果一条直线垂直于一个平面内的无数条直线,那么这条直线和这个平面垂直.②如果一条直线垂直于一个平面内的两条直线,那么这条直线和这个平面垂直.③如果一条直线不垂直于一个平面,则这条直线就不垂直于这个平面内的任何直线.④如果一条直线垂直于一个平面,那么这条直线有可能不垂直于这个平面内的某一条直线.A1个B2个C3个D4个