高中数学《余弦定理的证明》一、考题回顾
高中数学《余弦定理的证明》
一、考题回顾

一、考题回顾

参考解析
解析:二、考题解析
【教学过程】
(一)导入新课
情景导入:多媒体展示修路工人开凿山地隧道的情境图。提问:“为了测量山地隧道的长度,工人先在山顶选一个位置A,量出A点到隧道两端的距离AB、AC及AB与AC的夹角,最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设:已知三角形两边及其夹角,去求另一边的数学问题。
提问:“那工人们是如何算出来的呢?”
引发认知冲入,从而引出课题。

(四)小结作业
小结:通过这节课的学习,你有什么收获?
作业:课后题。
【板书设计】
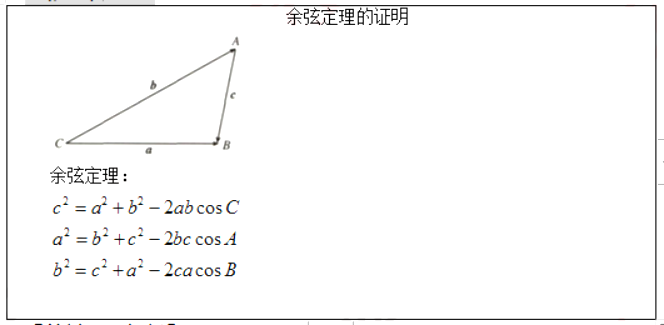
【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边,求三个角。
(2)已知两边和夹角,求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课,要从以下几个方面准备:
首先,备教材,教材分析是教师备好课、上好课的基本保证,对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提,更是教师进行教学研究的一种主要方法。
其次,备学生。教学的基本前提是为了学生而进行的教学,其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后,备教学方法。现代教学理论认为,在教学过程中,学生是学习的主体,教师是学习的组织者、引导者,教学的一切活动都必须以强调学生的主动性、积极性为出发点。
【教学过程】
(一)导入新课
情景导入:多媒体展示修路工人开凿山地隧道的情境图。提问:“为了测量山地隧道的长度,工人先在山顶选一个位置A,量出A点到隧道两端的距离AB、AC及AB与AC的夹角,最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设:已知三角形两边及其夹角,去求另一边的数学问题。
提问:“那工人们是如何算出来的呢?”
引发认知冲入,从而引出课题。

(四)小结作业
小结:通过这节课的学习,你有什么收获?
作业:课后题。
【板书设计】

【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边,求三个角。
(2)已知两边和夹角,求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课,要从以下几个方面准备:
首先,备教材,教材分析是教师备好课、上好课的基本保证,对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提,更是教师进行教学研究的一种主要方法。
其次,备学生。教学的基本前提是为了学生而进行的教学,其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后,备教学方法。现代教学理论认为,在教学过程中,学生是学习的主体,教师是学习的组织者、引导者,教学的一切活动都必须以强调学生的主动性、积极性为出发点。
相关考题:
下列关于高中数学基础性的说法不正确的是( )A.高中数学课程为学生进一步学习提高了必要的数学准备B.高中数学为不同学生提供相同的基础C.高中数学课程体现时代性、基础性和选择性D.高中数学课程要以学生的发展为本,尊重他们的个性发展
下列关于高中数学基础性的说法不正确的是()。A、高中数学课程为学生进一步学习提供了必要的数学准备B、高中数学课程为不同学生提供相同的基础C、高中数学课程体现时代性、基础性和选择性D、高中数学课程要以学生的发展为本,尊重他们的个性发展
下列关于高中数学课程结构的说法不正确的是()。A、高中数学课程可分为必修与选修两类B、高中数学选修课程包括4个系列的课程C、高中数学必修课程包括5个模块D、高中课程的组合具有固定性,不能发生改变
下列关于高中数学课程的变化内容,说法不正确的是()。A、高中数学课程中的向量既是几何的研究对象,也是代数的研究对象B、高中数学课程中,概率的学习重点是如何计数C、算法是培养逻辑推理能力的非常好的载体D、集合论是一个重要的数学分支
单选题下列关于高中数学课程的变化内容,说法不正确的是()。A高中数学课程中的向量既是几何的研究对象,也是代数的研究对象B高中数学课程中,概率的学习重点是如何计数C算法是培养逻辑推理能力的非常好的载体D集合论是一个重要的数学分支
单选题下列关于高中数学课程结构的说法不正确的是()。A高中数学课程可分为必修与选修两类B高中数学选修课程包括4个系列的课程C高中数学必修课程包括5个模块D高中课程的组合具有固定性,不能发生改变