关于正态分布理解不正确的是A.为左右对称的“钟形”曲线，又称高斯分布B.其统计学意义常以、SD和曲线下的概率来表示C.SD值越大，曲线越宽大，SD值越小，曲线越窄D.测定值位于±1SD范围内的概率为68%E.测定值位于±3SD之外的概率为5%
关于正态分布理解不正确的是
A.为左右对称的“钟形”曲线，又称高斯分布
B.其统计学意义常以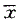
、SD和曲线下的概率来表示
C.SD值越大，曲线越宽大，SD值越小，曲线越窄
D.测定值位于
±1SD范围内的概率为68%
E.测定值位于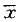
±3SD之外的概率为5%
B.其统计学意义常以
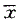、SD和曲线下的概率来表示C.SD值越大，曲线越宽大，SD值越小，曲线越窄
D.测定值位于
±1SD范围内的概率为68%E.测定值位于
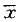±3SD之外的概率为5%参考解析
解析：本题考查正态分布中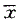
与SD的概率关系。测定值处于
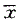±3SD范围内的概率为99.7%，之外应为0.3%；测定值处于
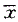+2SD范围内的概率为95.5%。
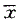与SD的概率关系。测定值处于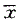±3SD范围内的概率为99.7%，之外应为0.3%；测定值处于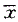+2SD范围内的概率为95.5%。
相关考题：
下列关于正态分布图的说法，正确的是( )。A．正态分布是描述离散型随机变量的一种重要概率分布B．整个曲线下的面积为1C．关于x=u对称，在x=u处曲线最高D．当u=a，a=1时，称正态分布为标准正态分布E．若固定u，a大时，曲线瘦而高
下列关于正态分布图的说法，正确的是（ ）。 A．正态分布是描述离散型随机变量的一种重要概率分布 B．整个曲线下的面积为l C．关于χ＝μ对称，在χ＝μ处曲线最高 D．当μ＝0，σ＝1时，称正态分布为标准正态分布 E．若固定μ，σ越大，曲线瘦而高
以下关于正态分布特征的描述，不正确的是A．正态分布为左右对称分布B．正态分布的两个参数：δ决定曲线向左或向右移动，μ决定曲线是“胖”还是“瘦”C．正态分布曲线均在横轴上方，在μ处最高D．标准正态分布是正态分布确定两个参数后的一个特例E．正态分布曲线下面积分布有一定规律
关于正态分布，错误的一项是A．标准正态分布的方差与标准差相同B．μ决定曲线的位置C．σ决定曲线的形状D．服从正态分布的变量在区间(μ- 3σ，μ+3σ)外取值的概率小于1%E．正态分布都可以通过变换化为标准正态分布
关于正态分布，错误的一项是A、标准正态分布的方差与标准差相同B、μ决定曲线的位置C、σ决定曲线的形状D、服从正态分布的变量在区间（μ－2σ，μ+2σ）外取值的概率小于1％E、正态分布都可以通过变换化为标准正态分布
关于正态分布的正确说法是（）。A、正态分布的失效率λ等于常数。B、正态分布具有对称性，它的主要参数是均值μ和方差σ2，记为N.μ，σ2）C、均值μ决定正态分布曲线的位置，代表分部的中心倾向。D、方差σ2决定正态分布曲线的形状，表征分布的离散程度。
关于正态分布，下列论述错误的是（）A、正态分布又称高斯分布B、正态分布是医学中最常用的一种连续性分布C、正态曲线的形态有μ椎一确定D、样本的频数分布对称，提示了总体可能服从正态分布E、检验资料是否服从正态分布最简单的办法是编制频数分布直方图
下列有关于正态分布说法不正确的是（）。A、.具有对称性也就是绝对值大小相等的正负误差出现的概率相等B、具有单峰性C、具有有界性D、正态分布曲线的位置和形状是由样本平均值和样本标准偏差两个参数确定
对于一般正态分布，如X~N（1，4），则有关该正态分布的概率密度曲线的叙述不正确的是（）。A、该分布的概率密度函数曲线关于x=1对称B、在x=1处达到最大值C、x轴为渐近线D、该概率密度函数曲线关于y轴对称
单选题关于正态分布，下列论述错误的是（ ）。A样本的频数分布对称，提示了总体可能服从正态分布B正态分布是医学中最常用的一种连续性分布C正态曲线的形态有μ惟一确定D正态分布又称高斯分布E检验资料是否服从正态分布最简单的办法是编制频数分布直方图
单选题以下关于正态分布特征的描述，不正确的是A正态分布为左右对称分布B正态分布的两个参数，σ决定曲线向左或向右移动，μ决定曲线是"胖"还是"瘦"C正态分布曲线均在横轴上方，在μ处最高D标准正态分布是正态分布确定两个参数后的一个特例E正态分布曲线下面积分布有一定规律
单选题关于t分布，哪项是错误的（）At分布是关于0对称的曲线B当u趋近于∞时，t分布为标准正态分布C与标准正态分布类似，t分布是唯一确定的一条曲线D相同υ，α越小，则ta，v越大Et分布是对称分布，但不是正态分布曲线
单选题以下关于正态分布特征的描述，不正确的是（ ）。A正念分布为左右对称分布B正态分布的两个参数σ决定曲线向左或向右移动，μ决定曲线是“胖”还是“瘦”C正态分布曲线均在横轴上方，在μ处最高D标准正态分布是正态分布确定两个参数后的一个特例E正态分布曲线下面积分布有一定规律
单选题关于正态分布的特征中，错误的是（ ）。A是中间高两边低B正态分布函数是一条光滑的钟形曲线C正态分布距离均值越近的地方数值越集中，在离均值较远的地方数值则很稀疏D正态分布密度函数越“瘦”，正态分布集中在均值附近的程度越小
填空题关于道德和法律的关系，以下理解不正确的是（）。