某消费者消费X和Y两种商品所获得的效用函数为:U=XY+Y,预算约束为:PX X + PYY = I,求: (1)若PX =2元,PY=1元,I=10元,求最大的总效用及收入边际效用(2)若PY上升到了4元,为保持问题(1)中的总效用不变,消费者需要花多少钱?
某消费者消费X和Y两种商品所获得的效用函数为:U=XY+Y,预算约束为:PX X + PYY = I,求: (1)若PX =2元,PY=1元,I=10元,求最大的总效用及收入边际效用
(2)若PY上升到了4元,为保持问题(1)中的总效用不变,消费者需要花多少钱?
(2)若PY上升到了4元,为保持问题(1)中的总效用不变,消费者需要花多少钱?
参考解析
解析:若PX =2元,PY=1元,I=10元则购买的两种商品量为X=2,Y=6 则总效用U=2·6+6=18
若PY上升到了4元,如果此时的收入变为I*,则购买两种商品量为:

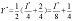
如果保持消费者在(3)问中的总效用不变的则XY+Y=18,把求出的两种商品的购买量代入,求出此时的收入水平为:I*=22,即消费者此时需要花费22元才能维持效用水平不变。
若PY上升到了4元,如果此时的收入变为I*,则购买两种商品量为:

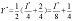
如果保持消费者在(3)问中的总效用不变的则XY+Y=18,把求出的两种商品的购买量代入,求出此时的收入水平为:I*=22,即消费者此时需要花费22元才能维持效用水平不变。
相关考题:
计算题:假定X和Y两种商品的效用函数为U= 计算题:假定X和Y两种商品的效用函数为U=,要求:(1)若X=5,则在总效用为10单位的无差异曲线上,对应的Y应为多少?这一商品组合对应的边际替代率是多少?(2)计算上述效用函数对应的边际替代率。
若MUx/Px>MUy/Py ,消费者应增加X商品的购买,减少Y商品的购买,最终可实现效用最大化。 若MUx/PxMUy/Py ,消费者应增加X商品的购买,减少Y商品的购买,最终可实现效用最大化。()
假定X和Y的价格PX和PY已知,当MRSXY>PX/PY时,消费者为达到效用最大化,他将()。 A、增加购买X,减少购买YB、减少购买X,增加购买YC、同时增加购买X,YD、同时减少购买X,Y
如果商品X对于商品Y的边际替代率MRSXY小于X和Y的价格之比PX/PY,则( )。A.该消费者应减少X消费,增加Y消费B.该消费者应增加X消费.减少Y消费C.单位货币购买x带来的边际效用大于单位货币购买Y带来的边际效用D.该消费者获得了最大效用
设某消费者的效用函数为柯布-道格拉斯类型的,即U=x^αy^β,商品x和商品y的价格分别为Px和Py,消费者收入为M,α和β为常数切α+β=1 (1)求该消费者关于商品x和商品y的需求函数。 (2)证明:当商品x和y的价格及消费者的收入均以相同的比例变化时,消费者对两商品的需求关系维持不变; (3)证明:该消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。
假设消费者对于苹果x和香蕉y的效用函数为:U(x,y)=(x+1)y。消费者的收入水平为I,苹果和香蕉的市场价格分别为px、和py。为追求效用最大化,求解消费者的马歇尔需求函数。香蕉是苹果的总替代品还是总互补品?
已知某消费者关于X、Y两商品的效用函数其中x、y分别对商品X、Y的消费量。 (1)求该效用函数关于X、y两商品的边际替代率表达式。 (2)在总效用水平为6的无差异曲线上,若x=3,求相应的边际替代率。 (3)在总效用水平为6的无差异曲线上,若x=4,求相应的边际替代率。 (4)该无差异曲线的边际替代率是递减的吗?
如果商品X对于商品Y的边际替代率MRS小于X和Y的价格之比PX/PY,则( )。A.该消费者应减少X消费,增加Y消费B.该消费者应增加X消费,减少Y消费C.该消费者未获得最大效用D.该消费者获得了最大效用
若消费者张某消费X和Y两种商品的效用函数U=X2Y2 ,张某收入为500元,X和Y的价格分别为PX =2元,PY=5元,求: (1)张某的消费均衡组合点。 (2)若政府给予消费者消费X以价格补贴,即消费者可以原价格的50%购买X,则张某将消费X和Y各多少? (3)若某工会愿意接纳张某为会员,会费为100元,但张某可以50%的价格购买X,则张某是否应该加入该工会?
假设Px和Py分别表示X和Y商品的价格,当边际替代率MRSxy大于Px/Py,消费者为达到最大效用,他将会()。A、增加X商品的购买,减少Y商品的购买B、减少X商品的购买,增加Y商品的购买C、同时增加或者减少X和Y商品的购买D、对X和Y商品的购买数量不发生改变
单选题假设Px和Py分别表示X和Y商品的价格,当边际替代率MRSxy大于Px/Py,消费者为达到最大效用,他将会()。A增加X商品的购买,减少Y商品的购买B减少X商品的购买,增加Y商品的购买C同时增加或者减少X和Y商品的购买D对X和Y商品的购买数量不发生改变
问答题若消费者张某消费X和Y两种商品的效用函数U=X2Y2 ,张某收入为500元,X和Y的价格分别为PX =2元,PY=5元,求: (1)张某的消费均衡组合点。 (2)若政府给予消费者消费X以价格补贴,即消费者可以原价格的50%购买X,则张某将消费X和Y各多少? (3)若某工会愿意接纳张某为会员,会费为100元,但张某可以50%的价格购买X,则张某是否应该加入该工会?
单选题假设消费者甲只消费商品X和Y,X的价格为PX=2,Y的价格为PY=5。如果甲达到了既定收入下的最大效用,则消费者甲的商品X和Y的边际效用之比为( )。A5/2B7/2C2/7D2/5E1/3