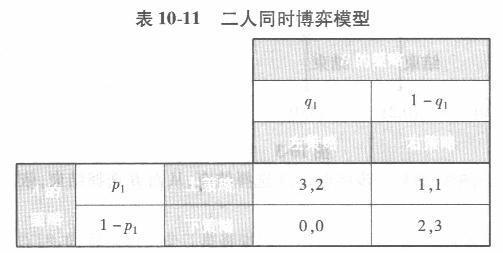
根据表10 -11的二人同时博弈模型,求: (1)参与人A与B的期望支付。 (2)参与人A与B的条件混合策略。 (3)纳什均衡。
根据表10 -11的二人同时博弈模型,求: (1)参与人A与B的期望支付。 (2)参与人A与B的条件混合策略。 (3)纳什均衡。

参考解析
解析:(1)由划线法可知参与人A与B的期望支付为: EA =3P1q1 +P1(1- q1)+2(1-P1)(1- q1) =4P1q1 -2q1 -P1 +2 =Pl (4q1 -1)- 2q1+2 EB =2P1q1 +P1(1- q1)+3(1-P1)(1- q1) =4P1q1 -2p1 -3q1 +3 =q1(4p1 -3)- 2p1+3 (2)参与人A与B的条件混合策略为:
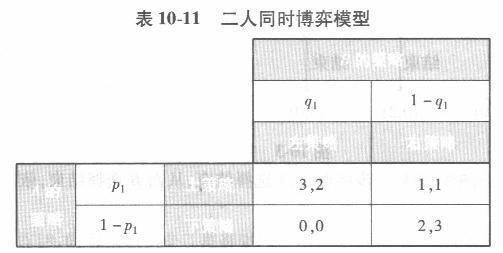
(3)纯策略纳什均衡为(3,2)(2,3),即(上,左)(下,右),混合策略纳什均衡为(3/4上,1/4左)如图10-5所示。
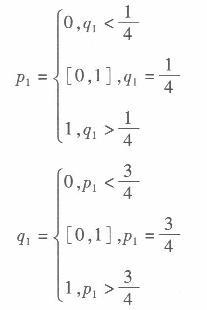

(3)纯策略纳什均衡为(3,2)(2,3),即(上,左)(下,右),混合策略纳什均衡为(3/4上,1/4左)如图10-5所示。
相关考题:
下列有关策略和纳什均衡的叙述错误的是().A.混合策略是博弈方根据一组选定的概率,在两种或两种以上可能的行为中随机选择的策略B.纯策略是博弈方采取一种选择或一种行动C.有些博弈不存在纯策略纳什均衡,但存在混合策略的纳什均衡D.有些博弈存在纯策略纳什均衡,但也存在混合策略的纳什均衡
不存在纯战略纳什均衡和存在惟一的纯战略纳什均衡,作为原博弈构成的有限次重复博弈,共同特点是重复博弈本质上不过是原博弈的简单重复,重复博弈的子博弈完美纳什均衡就是每次重复采用原博弈的纳什均衡。
多个纯战略纳什均衡博弈的有限次重复博弈子博弈完美纳什均衡路径:两阶段都采用原博弈同一个纯战略纳什均衡,或者轮流采用不同纯战略纳什均衡,或者两次都采用混合战略纳什均衡,或者混合战略和纯战略轮流采用。
单选题子博弈精炼纳什均衡的实质是().A所有参与人都是理性的B参与人行动存在先后顺序C重复剔除的占优均衡D以上都不对