用图说明短期生产函数Q=f(L,K)的TPL曲线、APL曲线和MPL曲线的特征及其相互之间的关系
用图说明短期生产函数Q=f(L,K)的TPL曲线、APL曲线和MPL曲线的特征及其相互之间的关系
参考解析
解析:短期生产函数的TPL曲线、APL曲线和MPL曲线的综合图如图4-5所示。
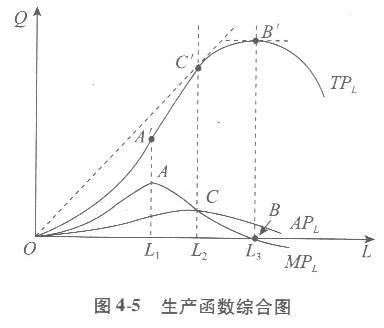
由图4-5可见,在短期生产的边际报酬递减规律的作用下,MPL曲线呈现出先上升达到最高点A以后又下降的趋势。由边际报酬递减规律决定的MPL曲线出发,可以方便地推导出TPL曲线和APL曲线,并掌握它们各自的特征及其相互之间的关系。 关于TPL曲线:由于MPL=dTPL/dL,所以当MPL >0时,随着变化收入的增加,TPL是增加的;当MPL <0时,TPL是减少的;而当MPL =0时,TPL曲线达到最高点。换言之,在L=L3时,MPL曲线达到零值的B点与TPL曲线达到最大值的B’点是相互对应的。此外,在LO的范围内,当MP’L>O时,TPL曲线的斜率递增,即TP。曲线以递增的速率上升;当MP’L<0时,TPL曲线的斜率递减,即TPL曲线以递减的速率上升;而当MP’=0时,TP。曲线存在一个拐点,换言之,在L=L1时,MPL曲线斜率为零的A点与TPL曲线的拐点4’是相互对应的。 关于APL曲线:由于APL=TPL/L,所以在L=L2时,TPL曲线有一条由原点出发的切线,其切点为C。该切线是由原点出发与TPL曲线上所有的点的连线中斜率最大的一条连线,故该切点对应的是APL的最大值点。再考虑到APr曲线和MPL曲线一定会相交在APL曲线的最高点.因此,在图4-5中,在L=L2时,APL曲线与MPL曲线相交于APL曲线的最高点C,而且与C点相对应的是TPL曲线上的切点C’。

由图4-5可见,在短期生产的边际报酬递减规律的作用下,MPL曲线呈现出先上升达到最高点A以后又下降的趋势。由边际报酬递减规律决定的MPL曲线出发,可以方便地推导出TPL曲线和APL曲线,并掌握它们各自的特征及其相互之间的关系。 关于TPL曲线:由于MPL=dTPL/dL,所以当MPL >0时,随着变化收入的增加,TPL是增加的;当MPL <0时,TPL是减少的;而当MPL =0时,TPL曲线达到最高点。换言之,在L=L3时,MPL曲线达到零值的B点与TPL曲线达到最大值的B’点是相互对应的。此外,在LO的范围内,当MP’L>O时,TPL曲线的斜率递增,即TP。曲线以递增的速率上升;当MP’L<0时,TPL曲线的斜率递减,即TPL曲线以递减的速率上升;而当MP’=0时,TP。曲线存在一个拐点,换言之,在L=L1时,MPL曲线斜率为零的A点与TPL曲线的拐点4’是相互对应的。 关于APL曲线:由于APL=TPL/L,所以在L=L2时,TPL曲线有一条由原点出发的切线,其切点为C。该切线是由原点出发与TPL曲线上所有的点的连线中斜率最大的一条连线,故该切点对应的是APL的最大值点。再考虑到APr曲线和MPL曲线一定会相交在APL曲线的最高点.因此,在图4-5中,在L=L2时,APL曲线与MPL曲线相交于APL曲线的最高点C,而且与C点相对应的是TPL曲线上的切点C’。
相关考题:
已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目前处于短期生产,且K=10,求:(1)写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。(2)分别计算当总产量TPL、劳动平均产量APL和劳动边际产量MPL各自达到极大值时的厂商劳动的投入量。(3)什么时候APL=MPL?它的值又是多少?
在短期内,生产划分为三个阶段,各个阶段的特征有( )。A、生产第一阶段的特征是MPL>APL>0B、生产第一阶段的特征是MPLC、生产第二阶段的特征是APL>MPLD、生产第二阶段的特征是APLE、生产第三阶段的特征是APL>MPL;MPL≤0
竞争性市场上有N个厂商,他们具有相同的生产技术,生产相同的产品,所需的投入为资本K和能源L。其中,资本的单位价格为R;由于能源受政府管制,单位价格为W不变。生产函数f(K,L) =AKαL1-α。求各企业的供给曲线和行业总供给曲线。 求各企业的供给曲线和行业总供给曲线。
已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目前处于短期生产切K的平均数为10 (1)写出在短期生产中该厂商关于劳动的总产量TPL函数、关于劳动的平均产量APL函数和关于劳动的边际产量MPL函数。 (2)分别计算当劳动的总产量TPL、劳动的平均产量APL和劳动的边际产量MPL各自达到最大值时的厂商的劳动投入量。 (3)什么时候APL= MPL?它的值又是多少?
假定一个竞争性厂商,其生产函数为Q=f(L,K)=AL^αK^β,生产要素L和K的价格分别为w和r。 (1)试求在K为不变投入时厂商的短期成本函数。 (2)求厂商的长期成本函数,并讨论不同的规模报酬对平均成本曲线形状的影响。
(1)在表中填空。 (2)根据(1),在一幅坐标图上作出TPL曲线,在另一幅坐标图上作出APL曲线和MPL曲线。(提示:为了便于作图与比较,TPL曲线图的纵坐标的刻度单位大于APL曲线图和MPL曲线图。) (3)根据(1),假定劳动的价格w=200,完成下面相应的短期成本表,即表5-2。(4)根据表5-2,在一幅坐标图上作出TVC曲线,在另一幅坐标图上作出AVC曲线和MC曲线。(提示:为了便于作图与比较,TVC曲线图的纵坐标的单位刻度大于AVC曲线图和MC曲线图。) (5)根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系。
生产的第二阶段应该:()A、开始于APL开始递减处(即APL的最高点),终止于MPL为零处B、开始于APL曲线和MPL曲线的相交处,终止于MPL曲线和水平轴的相交处C、开始于APL的最高点,终止于MPL为零处D、上述说法都对
对于生产函数Q=f(L,K)和成本方程C=wL+rK来说,在最优点生产要素组合点上应该有()A、等产量曲线和等成本线相切B、MRTSlk=w/rC、dk/dl=w/rD、MPl/MPk=w/r
已知生产函数Q=f(L,K)=4KL-L2-0.25K2,假定厂商目前处于短期生产,且K=20。 (1)写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。 (2)分别计算当劳动的总产量TPL、劳动的平均产量APL和劳动的边际产量MPL各自达到极大值时的厂商的劳动投入量。 (3)什么时候APL=MPL?它的值又是多少?
单选题假定总成本函数为TC=16+5Q+Q2,说明这是一条()。A短期成本曲线B长期成本曲线CC、B都对D无法确定