已知图示梁抗弯刚度EI为常数,则用叠加法可得跨中点C的挠度为:
已知图示梁抗弯刚度EI为常数,则用叠加法可得自由端C点的挠度为:
图示圆弧曲梁K截面轴力FNK(受拉为正),影响线C点竖标为( )。
图示结构EI=常数,不考虑轴向变形,MBA为(以下侧受拉为正)( )。
图示组合结构,梁AB的抗弯刚度为EI,二力杆的抗拉刚度都为EA。DG杆的轴力为( )。 A、0 B、P,受拉 C、P,受压 D、2P,受拉
如图(a)所示,该结构抗弯刚度为EI,取图(b)为基本结构,则δ11为( )。 A、l/(EI) B、5l/(6EI) C、9l/(16EI) D、l/(6EI)
如图所示的多跨静定梁,截面K的弯矩(以下侧受拉为正)Mk为( )kN·m。 A、5 B、6 C、9 D、13
图示结构B处弹性支座的弹性刚度k=3EI/l3,B结点向下的竖向位移为( )A.Pl3/(12EI)B.Pl3/(6EI)C.Pl3/(4EI)D.Pl3/(3EI)
图示结构K截面的弯矩值为(以内侧受拉为正)( )。A、PdB、-PdC、2PdD、-2Pd
图示结构,EI为常数。结点B处弹性支撑刚度系数k=3EI/L3,C点的竖向位移为( )。
图示结构B处弹性支座的弹簧刚度k=12EI/l3,B截面的弯矩为( )。A. Pl/2B. Pl/3C. Pl/4D. Pl/6
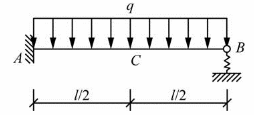
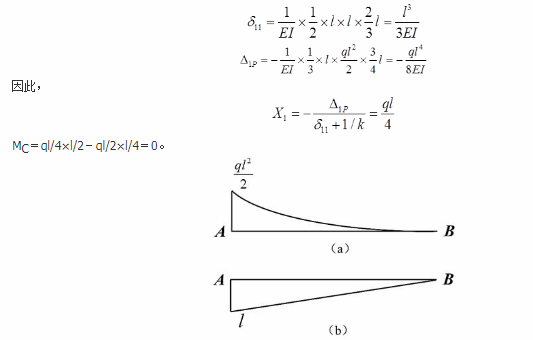
图示梁的抗弯刚度为EI,长度为l,欲使梁中点C弯矩为零,则弹性支座刚度k的取值应为( )
图示多跨梁截面C的弯矩为( )。A、M/2(上面受拉)B、M/2(下面受拉)C、3M/4(上面受拉)D、3M/4(下面受拉)
图示结构当水平支杆产生单位位移时(未注的杆件抗弯刚度为EI),B-B截面的弯矩值为( )。
图示圆弧曲梁K截面弯矩MK(外侧受拉为正)影响线C点竖标为( )。
图示结构K截面弯矩值为( )kN·m。A.0.5(上侧受拉)B.0.5(下侧受拉)C.1(上侧受拉)D.1(下侧受拉)
图示梁截面K的弯矩MK(以下侧受拉为正)等于:A. -10kN ? m B. -5kN ? m C. 0 D. 5kN
图示连续梁,中间支座截面的弯矩MB (以下侧受拉为正)等于:
图示连续梁,中间支座截面的弯矩MB(以下侧受拉为正)为( )。
图示简支梁跨中最大弯矩是( )kN·m。(下侧受拉为正)A.56B.88C.96D.116
假定下侧受拉为正,图示悬臂梁截面C处的弯矩是( )。A.-PaB.0C.PaD.2Pa
连续梁板的受力特点是()。A、跨中与支座均有正弯矩B、跨中与支座均有负弯矩C、跨中为负弯矩,支座为正弯矩D、跨中为正弯矩,支座为负弯
受弯梁内力计算中,关于弯矩正负号的规定正确的是()。A、顺时针为正B、逆时针为正C、使梁上侧受拉为正D、使梁下侧受拉为正
单选题图示结构K截面的弯矩值为(以内侧受拉为正)( )。A PdB -PdC 2PdD -2Pd
单选题连续梁板的受力特点是()。A跨中与支座均有正弯矩B跨中与支座均有负弯矩C跨中为负弯矩,支座为正弯矩D跨中为正弯矩,支座为负弯
多选题弯矩的符号一般规定以使梁的( )A下侧纤维受拉为正B上侧纤维受拉为负C没有符号之分D下侧纤维受拉为负E上侧纤维受拉为正