根据以上回归分析结果,最后得到的回归方程应为( )。
根据以上回归分析结果,最后得到的回归方程应为( )。
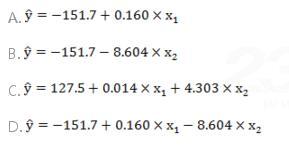
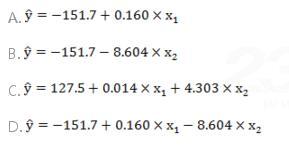
参考解析
解析:
相关考题:
根据下列资料编制直线回归方程 r= 0. 9 a=2.8() A. 直线回归方程yc= 2.8+ 1.08xB.直线回归方程yc= 2.8+ 1.18xC.直线回归方程yc= 0.9+ 1.08xD.直线回归方程yc= 0.9+1.18x
回归分析的正确步骤为() A、收集数据→绘制散布图→观察分析散布点→进行回归分析,建立回归方程→回归精度判断B、收集数据→观察分析散布点→绘制散布图→进行回归分析,建立回归方程→回归精度判断C、进行回归分析,建立回归方程→收集数据→绘制散布图→观察分析散布点→回归精度判断D、收集数据→回归精度判断→绘制散布图→观察分析散布点→进行回归分析,建立回归方程
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果根据表1~表3的输出结果可以得出( )。A.回归方程为:B.城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入和食品类居民消费价格指数的总体相关程度为87.7%C.多元回归分析中拟合优度大小应根据判定系数( )来衡量D.多元回归分析中拟合优度大小应根据调整后的判定系数( )来衡量
根据某地区1996-2015年的亩产量(公斤,y)、降雨量(毫米、x1)以及气温(度,x2)的统计数据进行回归分析,得到如下结果:R=0.9193,R2=0.8451,调整R2=0.8269对于回归方程来说,( )。A.t检验是检验解释变量xi对因变量y的影响是否显著B.t检验是从回归效果检验回归方程的显著性C.F检验是检验解释变量xi对因变量y的影响是否显著D.F检验是从回归效果检验回归方程的显著性
根据某地区1996-2015年的亩产量(公斤,y)、降雨量(毫米、x1)以及气温(度,x2)的统计数据进行回归分析,得到如下结果:R=0.9193,R2=0.8451,调整R2=0.8269多元回归方程的判定系数( )。A.等于0.8451B.等于0.8269C.统计含义是:亩产量的全部离差中,有84.51%可以由降雨量与气温的二元回归方程所解释D.统计含义是:亩产量的全部离差中,有82.69%可以由降雨量与气温的二元回归方程所解释
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果如果 ,根据表2,下列说法正确的是( )。A.F检验的假设为: B.F检验的假设为: C.回归方程的线性关系显著D.回归方程的线性关系不显著
根据下面资料,回答86-88题 某分析师认为美元走势对原油价格可能存在一定影响,他获取了最近的516个交易日的美元指数(x变量)和布伦特原油期货标牌价(y变量)数据并进行一元回归分析,结果如下: 据此回答以下三题。 得到的回归方程为( )。
在直线相关和回归分析中()。A、根据同一资料,相关系数只能计算一个B、根据同一资料,回归方程只能配合一个C、根据同一资料,回归方程随自变量与因变量的确定不同,可能配合两个D、回归方程和相关系数均与自变量和因变量的确定无关
根据下列资料编制直线回归方程r=0.9a=2.8()A、直线回归方程yc=2.8+1.08xB、直线回归方程yc=2.8+1.18xC、直线回归方程yc=0.9+1.08xD、直线回归方程yc=0.9+1.18x
回归分析预测法是指在分析市场现象的自变量和因变量之间相关关系的基础上,建立变量之间的回归方程,将回归方程作为预测模型,根据()在预测期的数量变化,预测因变量在预测期的变化结果的方法。A、预测值B、观察值C、权数D、自变量
回归分析预测法是指在分析市场现象的自变量和因变量之间相关关系的基础上,建立变量之间的(),将回归方程作为预测模型,根据自变量在预测期的数量变化,预测因变量在预测期的变化结果的方法。A、回归方程B、回归模型C、预测值D、观察值
多选题在直线相关和回归分析中()。A根据同一资料,相关系数只能计算一个B根据同一资料,回归方程只能配合一个C根据同一资料,回归方程随自变量与因变量的确定不同,可能配合两个D回归方程和相关系数均与自变量和因变量的确定无关