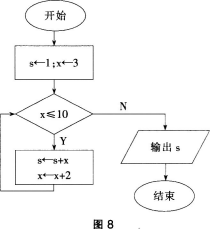
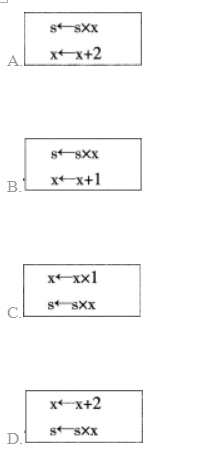
计算s=1+3+5+7+9的算法流程如图8所示,若要计算s=1×3×5×7×9,则下面流程图中的
计算s=1+3+5+7+9的算法流程如图8所示,若要计算s=1×3×5×7×9,则下面流程图中的




参考解析
解析:题中将s=1+3+5+7+9,改成计算s=1×3×5×7×9,变量x的步长还是2,所以应该修改为s←s×x,x←x+2。
相关考题:
有以下程序struct S{ int n; int a[20]; };void f(int *a,int n){ int i;for(i=0;in-1;i++) a[i]+=i;}main( ){ int i; struct S s={10,{2,3,1,6,8,7,5,4,10,9}};f(s.a,s.n);for(i=0;is.n;i++) printf("%d",s.a[i]);}程序运行后的输出结果是A)2,4,3,9,12,12,11,11,18,9,B)3,4,2,7,9,8,6,5,11,10,C)2,3,1,6,8,7,5,4,10,9,D)1,2,3,6,8,7,5,4,10,9,
有以下程序struct S {int n; int a[20];}; void f(struct S *P) {int i,j,t; for(i=0;in-1;i++) for(j=i+1;jn;j++) if(p-a[i]p-a[j]) { t=p-a[i]; p-a[i]=p-a[j]; p-a[j]=t; } } main() {int i; struct S s={10,{2,3,1,6,8,7,5,4,10,9}}; f(s); for(i=0;i printf(“%d”,s.a[i]); } 程序运行后的输出结果是( )。 A.1,2,3,4,5,6,7,8,9,10,B.10,9,8,7,6,5,4,3,2,1,C.2,3,1,6,8,7,5,4,10,9,D.10,9,8,7,6,1,2,3,4,5,
有以下程序struct S{ int n; int a[20]; }; void f(int *a,int n) {int i; for(i=0;i a[i]+=i; } main() {int i; struct S s={10,{2,3,1,6,8,7,5,4,10,9}}; f(s.a, s.n); for(i=0;i printf(“%d”,s.a[i]); } 程序运行后的输出结果是( )。A.2,4,3,9,12,12,11,11,18,9,B.3,4,2,7,9,8,6,5,11,10,C.2,3,1,6,8,7,5,4,10,9,D.1,2,3,6,8,7,5,4,10,9,
有以下程序 struct S { int n;int a[20];}; void f(int *a,int n) { int i; for(i=0;i<n-1;i++)a[i]+=i; } main() { int i;struct S s={10,{2,3,1,6,8,7,5,4,10,9}}; f(s.a,s.n); for(i=0;i<s.n;i++)printf("%d,",s.a[i]); } 程序运行后的输出结果是A.2,4,3,9,12,12,11,11,18,9,B.3,4,2,7,9,8,6,5,11,10,C.2,3,1,6,8,7,5,4,10,9,D.1,2,3,6,8,7,5,4,10,9,
下面程序段是计算()公式的。s=0:t=1Fori=1To10t=t*is=s+tNextiA.s=1+2+3+4+5+6+7+8+9+10B.s=1*2*3*4*5*6*7*8*9*10C.s=1!+2!+3!+4!+5!+6!+7!+8!+9!+10!D.s=1+2*3+3*4+4*5+5*6+6*7+7*8+8*9+9*10
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)~(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
阅读下列说明和流程图,将应填入(n)的字句写在对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…【流程图】计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。【流程图】
阅读以下说明和流程图,回答问题1和问题2。【说明】设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码B1B2…B7,可按下式计算偶校验位:其中,“”表示“异或”运算。下面的流程图描述了计算偶校验位的过程。【流程图】注:流程图中,循环开始的说明按照“循环变量名:循环初值,循环终值,增量”格式描述。将流程图中的(1)~(4)处补充完整。
阅读以下标准书号校验码的技术说明和程序流程图,根据要求回答问题1至问题3。[说明]为实现图书的国际统一编码,便于实现计算机化的图书管理,每本正式出版的图书都印有国际标准书号。标准书号由“ISBN”、10个数字(0~9)组成,其格式如下。ISBN 组号-出版者号-书名号-校验码其中,校验码是根据前面9个数字计算得到的,用于计算机自动校验。假设标准书号的10个数字依次是a(1),a(2),…,a(10),则校验码a(10)的设置应使S=10*a(1)+9*a(2)+8*a(3)+…+1*a (10)能被11整除。如果校验码a(10)应设置成10,则规定以“X”表示之。例如,《软件设计师考试考前冲刺预测卷及考点解析》的标准书号为:ISBN7-121-05027-5。第1段上的数字“7”是国际ISBN中心分配给中国ISBN中心管理的组号;第2段上的“121”表示电子工业出版社。标准书号的校验过程如图5-13所示,计算校验码的过程如图5-14所示。其中,Mod(S,11)表示S除以11得到的余数。请根据标准书号校验码的技术说明,将图5-13和图5-14程序流程图中(1)~(4)空缺处的内容填补完整。
●试题一阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…【流程图】图4计算并打印sinx的近似值。其中用ε(0)表示误差要求。
阅读以下说明和流程图,回答问题1和问题2。【说明】为便于管理,每本正式出版的图书都印有国际标准书号。标准书号由“ISBN”和 10个数字组成,其格式为:ISBN组号-出版者号-书名号-校验码。其中,校验码是根据前面9个数字计算得到的,用于计算机自动校验。假设标准书号的10个数字依次是 a(1),a(2),…,a(10),则校验码a(10)的设置应使S=10*a(1)+9*a(2)+8*a(3)+…1*a(10)能被 11整除。如果校验码a(10)应设置成10,则规定以“X”表示之。例如,信息处理技术员纲的标准书号为:ISBN 7-302-11191-X。第1段上的数字“7”是国际ISBN中心分配给中国ISBN中心管理的组号。第2段上的“302”表示清华大学出版社。标准书号的校验过程如图1-1所示,计算校验码的过程如图1-2所示,其中,Mod(S,11)表示S除以11得到的余数。【流程图】请填补流程图中的空缺(1)~(4)。
若采用白盒测试法对下面流程图所示算法进行测试,且要满足语句覆盖,则至少需要(51)个测试用例,若表示输入和输出的测试用例格式为(A,B,X;X),则满足语句覆盖的测试用例是(52)。 A. (1,3,3;8)B. (1,3,5;10) C. (5,2,15;8) D. (5,2,20;9)
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】
下面是一段关于计算变量s的算法: ①变量s的初值是0 ②变量i从1起循环到n,此时变量s的值由下面的式子表达式计算 ③s=s+(-1)*i ④输出变量s的值 这个计算s值的算法中,s的代数式表示是()。A、1-2+3-4+…+(-1)n*(n-1)B、1-2+3-4+…+(-1)n-1*nC、1+2+3+4+...+(n-1)+nD、-1-2-3-4-...-n