两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3,采用上述算法求解,则乘法次数为( )。A.156B.144C.180D.360
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
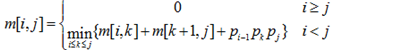
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3,采用上述算法求解,则乘法次数为( )。
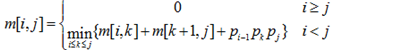
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3,采用上述算法求解,则乘法次数为( )。
A.156
B.144
C.180
D.360
B.144
C.180
D.360
参考解析
解析:四个矩阵分别为:
2*6 6*3
2*6 6*3
相关考题:
两个矩阵相乘,若矩阵总规模小于cache大小,则优化访存的最佳方法是____。 A、先将两个矩阵读入cache再进行乘法B、先转置第一个矩阵再进行乘法C、先转置第二个矩阵再进行乘法D、以上皆错
阅读下列函数说明和C函数,回答问题1~2,将解答填入栏内。[说明]若矩阵Am×n中存在某个元素aij满足:aij…是第i行中最小值且是第j列中的最大值,则称该元素为矩阵A的一个鞍点。下面程序的功能是输出A中所有鞍点,其中参数A使用二维数组表示,m和n分别是矩阵A的行列数。[程序]void saddle (int A[ ] [ ], int m, int n){ int i,j,min;for (i=0;i <m;i + + ){ min: (1);for (j=1; j<n; j+ +)if(A[i][j]<min) (2);for (j=0; j<n; j+ +)if ((3)){ p=0;while (p<m(4))p+ +;if (p > = m)printf ("%d,%d,%d\n",i,j,min);}}}[问题1] 将函数代码中的(1)~(4)处补充完整[问题2]在上述代码的执行过程中,若A为矩阵,则调用saddle(A,3,3)后输出是(5)。
试题四(15分)阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。【说明】某工程计算中要完成多个矩阵相乘(链乘)的计算任务。两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法,计算Am*n*Bn*p,需要m*n*p次乘法运算。矩阵相乘满足结合律,多个矩阵相乘,不同的计算顺序会产生不同的计算量。以矩阵A110*100,A2100*5,A35*50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。矩阵链乘问题可描述为:给定n个矩阵A1,A2,….An,矩阵Ai的维数为pi-1*Pi,其中i = 1,2,….n。确定一种乘法顺序,使得这n个矩阵相乘时进行乘法的运算次数最少。由于可能的计算顺序数量非常庞大,对较大的n,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若A1*A2*…*An的一个最优计算顺序从第k个矩阵处断开,即分为A1*A2*….Ak和Ak+1*Ak+2*…*An两个子问题,则该最优解应该包含A1*A2*…*Ak的一个最优计算顺序和Ak+1*Ak+2*…An的一个最优计算顺序。据此构造递归式,其中,cost[i][j]表示Ai+1*Ai+2*...Aj+1的最优计算的计算代价。最终需要求解cost[0][n-1]。【C代码】算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算3个矩阵、4个矩阵、…、n个矩阵相乘的最小计算量及最优计算顺序。下面是算法的C语言实现。(1)主要变量说明n:矩阵数seq[]:矩阵维数序列cost[][]:二维数组,长度为n*n,其中元素cost[i][j]表示Ai+1*Ai+2*…Aj+1的最优计算的计算代价trace[][]:二维数组,长度为n*n,其中元素trace[i][j]表示Ai+1*Ai+2*Aj+1的最优计算对应的划分位置,即k(2)函数cmmdefine N 100intcost[N][N];inttrace[N][N];int cmm(int n,int seq[]){int tempCost;int tempTrace;int i,j,k,p;int temp;for( i=0;in;i++){ cost[i][i] =0;}for(p=1;pn;p++){for(i=0; (1) ;i++){(2);tempCost = -1;for(k = i;kj;k++){temp = (3) ;if(tempCost==-1||tempCosttemp){tempCost = temp;(4) ;}}cost[i][j] = tempCost;trace[i][j] = tempTrace;}}return cost[0][n-1];}【问题1】(8分)根据以上说明和C代码,填充C代码中的空(1)~(4)。【问题2】(4分)根据以上说明和C代码,该问题采用了 (5) 算法设计策略,时间复杂度 (6) 。(用O符号表示)【问题3】(3分)考虑实例n=6,各个矩阵的维数:A1为5*10,A2为10*3,A3为3*12,A4为12*5,A5为5*50,A6为50*6,即维数序列为5,10,3,12,5,50,6。则根据上述C代码得到的一个最优计算顺序为 (7) (用加括号方式表示计算顺序),所需要的乘法运算次数为 (8) 。
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p 多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M{i+i),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( 64 )。若四个矩阵M1. M2、M3.,M4相乘的维度序列为2、6、3、10.3,采用上述算法求解,则乘法次数为( 65 )。A.O(N2)B.O(N2Lgn)C.O(N3)D.O(n3lgn)
已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(可以列出其递归式为其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为( ),算法的时间复杂度为( ),空间复杂度为(请作答此空)给定一个实例,(POPi........P5)=(20.15.4.10.20.25)最优计算顺序为( )A.O(n^2)B.O(n*2lgn)C.O(n^3)D.O(2n)
阅读下列说明和C代码,回答问题1至问题3【说明】 某工程计算中要完成多个矩阵相乘(链乘)的计算任务。 两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法,计算Am×n*Bn×p,需要m*n*p次乘法运算。 矩阵相乘满足结合律,多个矩阵相乘,不同的计算顺序会产生不同的计算量。以矩阵A110×100,A2100×5,A35×50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。 矩阵链乘问题可描述为:给定n个矩阵
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( )A.O(n2)B.O(n2lgn)C.O(n3)D.O(n3lgn)
已知阳阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(可以列出其递归式为其中,A 的维度为 pi-1*pi,m【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为(请作答此空),算法的时间复杂度为( ),空间复杂度为( )给定一个实例,(P0Pi........P5)=(20.15.4.10.20.25)最优计算顺序为( )A.分治法B.动态规划法C.贪心法D.回溯法
已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O(mnp)矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是(A*B)*C),也可以是A*(B*C).不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An(可以列出其递归式为其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为( ),算法的时间复杂度为( ),空间复杂度为( )给定一个实例,(POPi........P5)=(20.15.4.10.20.25)最优计算顺序为(请作答此空)A.(((A1*A2)*A3)*A4)*A5B.A1*(A2*(A3*(A4*A5)))C.((A1*A2)*A3)*(A4*A5)D.(A1*A2)*((A3*A4)*A5)
如果用A代表银行业务发生某种经济损失的随机事件,N代表统计观测次数,M代表A发生的次数,P(A)代表A的概率。则下列哪个公式正确()A、P(A)=MNB、P(A)=M/NC、P(A)=N/MD、P(A)=M+N
单选题矩阵的乘法不满足哪一规律?()A结合律B分配律C交换律D都不满足