对于非空的二叉树,设D代表根结点,L代表根结点的左子树R代表根结点的右子树。若对下图所示的二叉树进行遍历后的结点序列为7 6 5 4 3 2 1,则遍历方式是( )。A.LRDB.DRLC.RLDD.RDL
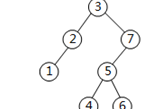
对于非空的二叉树,设D代表根结点,L代表根结点的左子树R代表根结点的右子树。若对下图所示的二叉树进行遍历后的结点序列为7 6 5 4 3 2 1,则遍历方式是( )。

A.LRD
B.DRL
C.RLD
D.RDL
B.DRL
C.RLD
D.RDL
参考解析
解析:该题突破了常规的遍历树的方式,采用了新的遍历方式。但是做题进行判断时还是比较容易的,因为先根(包括根左右与根右左)的遍历,则根结点3会是第1个访问的结点;后根(左右根与根右左)的遍历,则根结点3会是最后1个访问的结点。给出的序列中3既不在第1个位置,也不在最后1个位置,所以先根后根都可除排,而A、B、C三个选项中,A与C是后根,B选项是先根,都可排除,只能选D。D是右根左的访问方式,与结点序列完全吻合。
相关考题:
●二叉排序树或者是一棵空树,或者是具有如下性质的二叉树:若其左子树非空,则左子树上所有结点的值均小于根结点的值;若其右子树非空,则右子树上所有结点的值均大于根结点的值;其左、右子树本身就是两棵二叉排序树。根据该定义,对一棵非空的二叉排序树进行 (42)遍历,可得到一个结点元素的递增序列(42)A. 先序(根、左、右)B. 中序(左、根、右)C. 后序(左、右、根)D. 层序(从树根开始,按层次)
阅读以下说明和C语言函数,将应填入(n)处的字句写在答题纸的对应栏内。【说明】一棵非空二叉树中“最左下”结点定义为:若树根的左子树为空,则树根为“最左下”结点;否则,从树根的左子树根出发,沿结点的左子树分支向下查找,直到某个结点不存在左子树时为止,该结点即为此二叉树的“最左下”结点。例如,下图所示的以 A为根的二叉树的“最左下”结点为D,以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下:typedef stmct BSTNode{int data;struct BSTNode*lch,*rch;//结点的左、右子树指针}*BSTree;函数BSTree Find Del(BSTree root)的功能是:若root指向一棵二叉树的根结点,则找出该结点的右子树上的“最左下”结点*p,并从树于删除以*p为根的子树,函数返回被删除子树的根结点指针;若该树根的右子树上不存在“最左下”结点,则返回空指针。【函数】BSTrce Find_Del(BSTreeroot){ BSTreep,pre;if ( !root ) return NULL; /*root指向的二叉树为空树*/(1); /*令p指向根结点的右子树*/if ( !p ) return NULL;(2); /*设置pre的初值*/while(p->lch){ /*查找“最左下”结点*/pre=p;p=(3);}if ((4)==root) /*root的右子树根为“最左下”结点*/pre->rch=NULL;else(5)=NULL; /*删除以“最左下”结点为根的子树*/reurn p;}
前序遍历序列与中序遍历序列相同的二叉树为(1),前序遍历序列与后序遍历序列相同的二叉树为(2)。A.根结点无左子树的二叉树B.根结点无右子树的二叉树C.只有根结点的二叉树或非叶子结点只有左子树的二叉树D.只有根结点的二叉树或非叶子结点只有右子树的二叉树
● 满二叉树的特点是每层上的结点数都达到最大值,因此对于高度为 h(h1)的满二叉树,其结点总数为 (36) 。对非空满二叉树,由根结点开始,按照先根后子树、先左子树后右子树的次序,从 1、2、3、…依次编号,则对于树中编号为 i 的非叶子结点,其右子树的编号为 (37) (高度为 3 的满二叉树如下图所示) 。
满二叉树的特点是每层上的结点数都达到最大值,因此对于高度为h(h>1)的满二叉树,其结点总数为(36)。对非空满二叉树,由根结点开始,按照先根后子树、先左子树后右子树的次序,从1、2、3、…依次编号,则对于树中编号为i的非叶子结点,其右子树的编号为(37)(高度为3的满二叉树如下图所示)。A.2hB.2h-1C.2h-1D.2h-1+1
某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是( )。A.A,I.KB.F,IC.F,GD.I,G
后序遍历序列与中序遍历序列相同的二叉树为(85),前序遍历序列与后序遍历序列相同的二叉树为(86)。A.根结点无左子树的二叉树B.根结点无右子树的二叉树C.只有根结点的二叉树或非叶子结点只有左子树的二叉树D.只有根结点的二叉树或非叶子结点只有右子树的二叉树
一棵二叉树满足下列条件:对任一结点,若存在左、右子树,则其值都小于它的左子树上所有结点的值,而大于右子树上所有结点的值。现采用【 】遍历方式就可以得到这棵二叉树所有结点的递增序列。A.先根B.中根C.后根D.层次
对二叉树进行后序遍历和中序遍历时,都依照左子树在前右子树在后的顺序。已知对某二叉树进行后序遍历时,结点M是最后被访问的结点,而对其进行中序遍历时,M是第一个被访问的结点,那么该二叉树的树根结点为M,且( )。A.其左子树和右子树都必定为空B.其左子树和右子树都不为空C.其左子树必定为空D.其右子树必定为空
某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为 HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是(37)A.A,I.K B. F,I C. F,G D.I,G
先序遍历序列和中序遍历序列相同的二叉树为()。A.根结点无左子树的二叉树B.根结点无右子树的二叉树C.只有根结点的二叉树或非子结点只有左子树的二叉树D.只有根结点的二叉树或非叶子结点只有右子树的二叉树
已知某二叉树的先序遍历序列为A B C D E F、中序遍历序列为B A D C F E,则可以确定该二叉树( )。A.是单支树(即非叶子结点都只有一个孩子)B.高度为4(即结点分布在4层上)C.根结点的左子树为空D.根结点的右子树为空
多选题二叉树的中序遍历序列是E、B、A、C、F、D,若A是根结点,则E结点不可能在()。A左子树B右子树C右子树的第二层D右子树的根节点