多个样本率比较χ检验中，若P≤a，拒绝H，接受H，所得的结论是A.多个总体率全不相等B.多个样本率全相等C.多个样本率不全相等D.多个总体率全相等E.多个总体率不全相等
多个样本率比较χ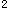
检验中，若P≤a，拒绝H
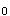，接受H
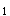，所得的结论是
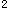检验中，若P≤a，拒绝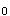H，接受H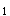，所得的结论是A.多个总体率全不相等
B.多个样本率全相等
C.多个样本率不全相等
D.多个总体率全相等
E.多个总体率不全相等
B.多个样本率全相等
C.多个样本率不全相等
D.多个总体率全相等
E.多个总体率不全相等
参考解析
解析：
相关考题：
若得P0.05，则结论是A．不拒绝Ho，两样本率相等B．拒绝Ho，两样本率不等C．接受Ho，样本率与总体率相等D．不拒绝Ho，尚不能认为样本所在地的总体率高于我国平均阳性率E．拒绝Ho，样本率与总体率不等
假设检验中，若P＞0.05，其正确解释是A．如果H0成立，抽得现有样本差别的概率不算小，故只能接受H0B．检验假设成立的可能性很小，属小概率事件C．备择假设H1成立的可能性P＞0.05，故应予以接受D．在H0成立的前提下，很可能出现两样本均数不等的情况E．如果H0成立，抽得现有样本差别的概率不算小，按现有检验水平应拒绝H0
当多个样本率比较的χ检验推断结论为拒绝H0接受H0时要进一步推断哪两个总体率有差别用那种方法:()。 A、直接用四格表资料的χ检验进行多重比较B、χ分割法把R×表分割成多个独立的四格表进行两两比校正检验水准αC、不能比较D、χ分割法把R×表分割成多个独立的四格表进行两两比较，检验水准α不变
当多个样本率比较的χ检验推断结论为拒绝H0接受H0时可认为:()。 A、多个样本总体率不同多个样本总体率两两不同B、多个样本总体率相同多个样本总体率两两不同C、多个样本总体率相同D、多个样本总体率不同个样本两两总体率不一定不同
在两样本比较的秩和检验中，已知第1组的样本量为n1=10，秩和T1=136，第2组的样本量为n2=15，秩和T2=189，若双侧0.05的T界值范围为94～166，按α=0.05，作出的统计推断是A．94＜T2，P＜0.05，拒绝H0B．T1＜166，P＞0.05，不拒绝H0C．T2＞166，P＜0.05，拒绝H0D．94＜T1，P＜0.05，拒绝H0E．94＜T1＜166，P＞0.05，不拒绝H0
从某个城市中随机抽取15个家庭组成一个随机样本，得到样本均值为84．50元，标准差为14．50元。在μ=0．05的显著性水平下，检验假设H0：μ=90，H1：μ≠90，得到的结论是( )。A.拒绝H0B.不拒绝H0C.可以拒绝也可以接受H0D.可能拒绝也可能接受H0
若得P0．05，则结论是A.不拒绝H。，两样本率相等B.拒绝H。，两样本率不等C.接受H。，样本率与总体率相等D.不拒绝H。，尚不能认为样本所在地的总体率高于我国平均阳性率E.拒绝H。，样本率与总体率不等
经过统计得到X＞X结果，正确的结论是A.P＝0.05，拒绝H，差异有统计学意义B.P＞0.05，接受H，的可能性较大C.P＝0.05，接受H，差异无统计学意义D.P＜0.05，拒绝H，差异有统计学意义E.P＞0.05，接受H，差异无统计学意义
经过统计得到X2>X20.05结果，正确的结论是A.P=0.05，拒绝H，差异有统计学意义B.P>0.05，接受H，的可能性较大C.P=0.05，接受H，差异无统计学意义D.P＜0.05，拒绝H，差异有统计学意义E.P>0.05，接受H，差异无统计学意义
假设检验时，若α=0.05，则下列关于检验结果的说法正确的是A.若P大于0.05，则拒绝H，此时可能犯Ⅰ型错误B.若P小于0.05，则拒绝H，此时可能犯Ⅱ型错误C.若P小于0.05，则不拒绝H，此时可能犯Ⅰ型错误D.若P小于0.05，则不拒绝H，此时可能犯Ⅱ型错误E.若P大于0.05，则不拒绝H，此时可能犯Ⅱ型错误
假设检验中，若P>0．05，其正确解释是A.如果H成立，抽得现有样本差别的概率不算小，按现有检验水平应拒绝HB.在H成立的前提下，很可能出现两样本均数不等的情况C.检验假设成立的可能性很小，属小概率事件D.如果H成立，抽得现有样本差别的概率不算小，故只能接受HE.备择假设H成立的可能性P>0．05，故应予以接受
两个大样本比较的Z检验，计算得Z=2.58(取双侧a=0.05)，则A.P=0.05，拒绝HB.P＜0.05，不拒绝HC.P＜0.05，拒绝HD.P>0.05，不拒绝HE.P>0.05，拒绝H
在两样本比较的秩和检验中，已知第1组的样本量为n=10，秩和T=170，第2组的样本量为n=12，秩和T=83，若界值范围为85～145，则作出的统计推断是A.85＜T，P＜0.05，拒绝HB.T＜85，P>0.05，拒绝HC.85＜T2＜145，P＜0.05，拒绝HD.T＜85，P＜0.05，不拒绝HE.T>145，P＜0.05，拒绝H
我国人群HBsAg阳性率平均为10%，某地随机抽查了100人，其中HBsAg阳性20人若得P>0.05，则结论是A.接受H，样本率与总体率相等B.不拒绝H，尚不能认为样本所在地的总体率高于我国平均阳性率C.拒绝H，两样本率不等D.拒绝H，样本率与总体率不等E.不拒绝H，两样本率相等
从某个城市中随机抽取15个家庭组成一个随机样本，得到样本均值为84.50元，标准差为14.50元。在α=0.05的显著性水平下，检验假设H0：μ=90，H1：μ≠90，得到的结论是（）。A、拒绝H0B、接受H0C、可以拒绝也可以接受H0D、可能拒绝也可能接受H0
关于行×列表资料的卡方检验，正确的是（）。A、不能用于四格表资料的分析B、只能用于多个样本率的比较C、可用于交叉分类资料两种属性间关联性分析D、对多个样本率作比较若拒绝H0，表明任两个总体率不相等E、能用于多个构成比的比较
在两样本比较的秩和检验中，已知第1组的样本量为n1=10，秩和T1=136，第2组的样本量n2=15，秩和T2=189，若双侧0．05的T界值范围为94～166，按α=0．05，作出的统计推断是（）A、94，P0.05，拒绝H0B、94166，P0.05，不拒绝H0C、T2166，P0.05，拒绝H0D、94，P0.05，拒绝H0E、94166，P0.05，不拒绝H0
两个大样本比较的Z检验，计算得Z=2.58（取双侧a=0.05），则（）A、P0.05，不拒绝H0B、P0.05，不拒绝H0C、P0.05，拒绝H0D、P0.05，拒绝H0E、P=0.05，拒绝H0
在两样本比较的秩和检验中，已知第1组的样本量为n1=10，秩和T1=170，第2组的样本量为n=12，秩和T=83，若界值范围为85～145，则作出的统计推断是（）A、85，P0.05，拒绝H0B、T85，P0.05，不拒绝H0C、T85，P0.05，拒绝H0D、85E、T145，P0.05，拒绝H0
已知三个样本率，P1、P2和P3，对应的总体率用和表示，拟做三个样本率比较的X2检验，则正确的是（）。A、H0：H1：B、若X2统计量很大，则P便很小，说明和间差别很大。C、若拒绝H0可认为和两两均不相等。D、若X2统计量非常小，则P便较大，当时不拒绝H0，也可能犯错误。E、上述均不对
单选题在两样本比较的秩和检验中，已知第1组的样本量为n1=10，秩和T1=170，第2组的样本量为n=12，秩和T=83，若界值范围为85～145，则作出的统计推断是（）A85，P0.05，拒绝H0BT85，P0.05，不拒绝H0CT85，P0.05，拒绝H0D85ET145，P0.05，拒绝H0
单选题检验假设H0：μ≤50，H1：μ＞50，随机抽取一个n=16的样本，得到的统计量的值为t=2.5，在α=0.05的显著性水平下，得到的结论是（ ）。A拒绝H0B接受H0C可以拒绝也可以接受H0D可能拒绝也可能接受H0
多选题关于行×列表资料的卡方检验，正确的是（）。A不能用于四格表资料的分析B只能用于多个样本率的比较C可用于交叉分类资料两种属性间关联性分析D对多个样本率作比较若拒绝H0，表明任两个总体率不相等E能用于多个构成比的比较
单选题在两样本比较的秩和检验中。已知第1组的样本量为n1=8，秩和T1=170，第2组的样本量为n2=12，秩和T2=83，若界值T0.5(10,4)=85～145，则作出的统计推断是（ ）。A85＜T2＜145，P＜0.05，拒绝H0BT2＜85，P＜0.05，不拒绝H0CT2＜85，P＞0.05，拒绝H0D85＜T1，P＜0.05，拒绝H0ET1＞145，P＜0.05，拒绝H0
单选题假设检验时，若α=0.05，则下列关于检验结果的说法正确的是（）A若P大于0.05，则拒绝H0，此时可能犯Ⅰ型错误B若P小于0.05，则拒绝H0，此时可能犯Ⅱ型错误C若P小于0.05，则不拒绝H0，此时可能犯Ⅰ型错误D若P小于0.05，则不拒绝H0，此时可能犯Ⅱ型错误E若P大于0.05，则不拒绝H0，此时可能犯Ⅱ型错误