图示结构，由细长压杆组成，各杆的刚度均为EI，则P的临界值为：

图示结构，由细长压杆组成，各杆的刚度均为EI，则P的临界值为：

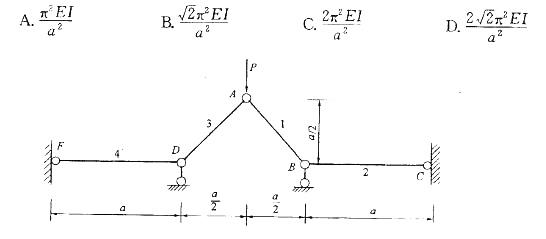
参考解析

解析：提示：由静力平衡可知两点的支座反力为P/2，方向向上。首先求出1、3杆的临界力Pcr1，由结点A的平衡求出[P]1的临界值；再求出2、4杆的临界力Pcr2，由结点B的平衡求出[P]2的临界值。比较两者取小的即可。

相关考题：

图示结构两杆长均为d,EI=常数。则A点的水平位移为()A.(←)pd³/2B.Pd3/3EI(→)C.Pd3/3EI(←)D.Pd3/6EI(→)
查看答案
图示结构两杆长均为d,EI=常数。则A点的垂直位移为()A.qd3/2EI(↑)B.qd3/3EI(↓)C.qd4/4EI(↓)D.qd4/6EI(↓)
查看答案
五根等长的细直杆铰结成图示杆系结构，各杆重力不计。若PA=PC=P，且垂直BD。则杆BD内力SBD为：
查看答案
图示矩形截面细长(大柔度)压杆，弹性模量为E。该压杆的临界荷载Fcr为：
查看答案
图示四根细长（大柔度）压杆，弯曲刚度均为EI。其中具有最大临界荷载Fcr的压杆是（　　）。A．图（A）B．图（B）C．图（C）D．图（D）
查看答案
图示三根压杆均为细长（大柔度）压杆，且弯曲刚度均为EI。三根压杆的临界荷载Fcr的关系为：A. Fcra>Fcrb>FcrcB.Fcrb>Fcra>FcrcC. Fcrc>Fcra>FcrbD.Fcrb>Fcrc>Fcra
查看答案
图示结构，由细长压杆组成，各杆的刚度均为EI，则P的临界值为：
查看答案
图示三根压杆均为细长（大柔度）压杆，且弯曲刚度均为EI。三根压杆的临界载荷Fcr的关系为（　　）。 A． Fcra＞Fcrb＞Fcrc B． Fcrb＞Fcra＞Fcrc C． Fcrc＞Fcra＞Fcrb D． Fcrb＞Fcrc＞Fcra
查看答案
两个结构受力如图所示。AB、CD梁的抗弯刚度均为EI，而BD杆的抗拉(压)刚度均为EA。若用Na和Nb分别表示两结构中杆的轴力，则下列结论中正确的是： A.Na=Nb B.NabC. Na>Nb D.无法比较Na和Nb的大小
查看答案
两根完全相同的细长（大柔度）压杆AB和CD如图所示，杆的小端为固定铰链约束，上端与刚性水平杆同结。两杆的弯曲刚度均为EI，其临界载荷Fa为;
查看答案
两根完全相同的细长（大柔度）压杆AB和CD如图所示，杆的下端为固定铰链约束，上端与刚性水平杆固结。两杆的弯曲刚度均为EI，其临界载荷Fa为：
查看答案
图示矩形截面细长(大柔度)压杆，弹性模量为E。该压杆的临界载荷Fσ
查看答案
在图示体系中，集中质量为m，杆长为l，抗弯刚度为EI，杆重不计。该体系自由振动的周期为（　　）。
查看答案
图示结构，质量m在杆件中点，EI＝∞，弹簧刚度为k，该体系自振频率为（　　）。
查看答案
图示组合结构，梁AB的抗弯刚度为EI，二力杆的抗拉刚度都为EA。DG杆的轴力为（　　）。 A、0 B、P，受拉 C、P，受压 D、2P，受拉
查看答案
图示刚架，各杆线刚度相同，则结点A的转角大小为（　　）。
查看答案
图示各结构中，除特殊注明者外，各杆EI=常数。其中不能直接用力矩分配法计算的结构是：
查看答案
图示结构，各杆EI、EA相同，K、H两点间的相对线位移为:
查看答案
图示结构当水平支杆产生单位位移时（未注的杆件抗弯刚度为EI），B-B截面的弯矩值为（　　）。
查看答案
图示结构，汇交于A点的各杆端转动刚度系数之和设为，则杆A端的力矩分配系数为：
查看答案
图示为结构在荷载作用下的M图，各杆EI=常数，则支座B处截面的转角为:
查看答案
图示结构各杆EI=常数，杆端弯矩MDE:
查看答案
图示结构各杆EI=常数，其C端的水平位移(→)为:
查看答案
图示三根压杆均为细长(大柔度)压杆，且弯曲刚度均为EI。三根压杆的临界荷载Fcr的关系为：
查看答案
图示结构中，除横梁外各杆件EI=常数。质量集中在横梁上，不考虑杆件的轴向变形，则体系振动的自由度数为（） A1B2C3D4
查看答案
用力矩分配法计算图示结构，并绘出弯矩图。各杆EI相同且为常数。
查看答案
用力法计算图示结构，并作弯矩图。各杆EI相同且为常数。
查看答案
图示结构中，除横梁外，各杆件EI=常数。不考虑杆件的轴向变形，则体系振动的自由度数为1 A对B错
查看答案
热门标签