华东师大版八年级数学上册 13.5.2 线段垂直平分线 导学案(无答案)
A.同素性
B.定比性
C.平行性
D.从属性
此题为判断题(对,错)。
A、同素性
B、全等性
C、定比性
D、从属性
根据平面图形中所标注的尺寸及线段连接关系,图形中线段可分为已知线段、中间线段、连接线段、末端线段。()
A、单线段;间距2mm的双直线段且涂实心;间距为2mm的双直线段(空心)
B、单线段;间距为1mm的双直线段且涂实心;间距为1mm的双直线段(空心)
C、间距为2mm的双直线段且涂实心;单线段;间距为2mm的双直线段(空心)
D、间距为1mm的双直线段且涂实心;单线段;间距为1mm的双直线段(空心)
县新时代国际学校导学案课时及内容:13.5.2线段垂直平分线 课型:新授课 姓名:_组号:_年级: 八年级 学科: 数学 执笔人: 审核人: 使用日期:_ 学习目标:1、初步掌握线段的垂直平分线的性质定理及其逆定理;2、会运用线段垂直平分线的性质定理及逆定理解决有关问题.学习过程:预学案-“凡事预则立不预则废”使用说明学法指导:1、依据预习案,通读教材,进行知识梳理;勾画重点,写上提示语、标注。2、将预习中不能解决的问题标识出来,并填写在后面“我的疑惑”中。3、预习课本94-95页,限时5分钟,独立完成预习自测。预习自测:-本部分考查课本基础知识,内容相对简单,只有“用心才会,细心才对”。一、 知识回顾:1、线段垂直平分线的定义: BA2尺规作已知线段AB的垂直平分线MN:二、新知导入: 在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?由此你能得出什么规律?我的疑惑:请将你预习中未能解决的问题和有疑惑的问题写在下面,待课堂上和老师同学们一起探究解决。探究案:-学始于疑、我思故我在。1.命题:线段垂直平分线上的点到 .PABMC2.试证明上述命题.已知,如图直线MNAB,垂足是C,且AC=CB.点P在MN上N求证:PA=PB由此可得:线段垂直平分线性质定理: . ABP3.上述定理的逆命题: . 已知,如图PA=PB,求证:点P在线段AB的垂直平分线上逆定理: .PA=PB点P在线段AB的垂直平分线上到线段两个端点距离相等的点,在这条线段的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等训练案-有效训练,当堂矫正。试一试,1、求证:三角形三边的垂直平分线交于一点。A2、已知:如图,D是BC延长线上的一点,BD=BC+AC. 求证:点C在AD的垂直平分线上.DCB3如图,ABC的周长为19cm,且BCAC,BC的垂直平分线DE交AC于E,D为垂足,AB5cm,求ABE的周长。
下列各命题都成立,写出它们的逆命题。这些逆命题成立吗?(1)两直线平行,同位角相等;(2)如果两个实数是正数,那么它们的积是正数;(3)等边三角形是锐角三角形;(4)线段垂直平分线上的点到这条线段两个端点的距离相等。
解:
(1)同位角相等,两直线平行。 逆命题成立
(2)如果两个实数的积是正数,那么两个实数都是正数 逆命题不成立
(3)锐角三角形是等边三角形 逆命题不成立
(4)到一条线段两个端点的距离相等的点在线段垂直平分线上 逆命题不成立
已知点A(-4,2),B(0,o),则线段AB的垂直平分线的斜率为 ( )

A.A
B.B
C.C
D.D
本题主要考查的知识点为线段垂直平分线的斜率.【应试指导】
【应试指导】设线段的垂直平分线上任一点为P(χ,y),则

即

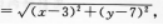
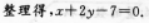
B.-7
C.3
D.1
E.2
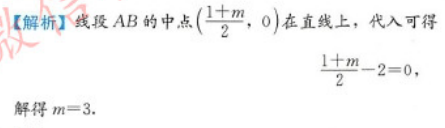
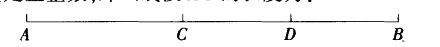
B.3
C.5
D.7

相关考题:
- 解释氧化还原反应中还原剂的概念?
- 单选题主要和CDK2的抑制有关的CKIs是( )。ABCDE
- 在制氢站、氢冷设备、储氢罐等处进行检修工作时,应使用(),以防止产生火花。A、铁制工具;B、铜制工具;C、木制工具;D、钢制工具。
- 单选题The Serial ATA (SATA) cables can extend up to ().A10 metersB5 metersC1 meterD100 metersE15 meters
- 填空题2019年7月15日至16日,习近平总书记在内蒙古考察并指导开展“不忘初心、牢记使命”主题教育时指出,新时代加强精神文明建设,要坚持文艺()、()的方向,积极支持和推广直接为基层老百姓服务的文艺活动。
- 按照漏氢部位来分,氢冷发电机漏氢有哪几种表现形式?
- 单选题Bluetooth is a ()technology.ASatelliteBMicrowaveCLight waveDRadio Frequency
- 将交流电变换成直流电的过程叫()。A、逆变;B、电解;C、充电;D、整流。
- 为什么选择氢氧化钠、氢氧化钾作为电解质?
- 单选题Which of the following storage devices is not an example of an optical storage device?()ABlu-RayBDVDCSSDDCD