袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是________.
袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是________.
参考解析
解析:一般理解随机事件“第二个人取得黄球”与第一个人取得的是什么球有关,这就要用全概率公式来计算,但也可以用古典型概率来解,这会简单得多.(方法一)设事件Ai表示第i个人取得黄球,i=1,2,则根据全概率公式:

(方法二)只考虑第二个人取得的球,这50个球中每一个都会等可能地被第二个人取到,而取到黄球的可能有20个,故所求概率为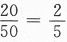

(方法二)只考虑第二个人取得的球,这50个球中每一个都会等可能地被第二个人取到,而取到黄球的可能有20个,故所求概率为
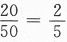
相关考题:
从甲袋内摸出一个白球的概率是1/3,从乙袋内摸出一个白球的概率是1/2,从两个袋内各摸出一个球,那么________等于1/6。A.2个球都是白球的概率B.2个球都不是白球的概率C.2个球不都是白球的概率D.2个球中恰有1个白球的概率
一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋,其中3只黄球,4只白球。他随机取出一只乒乓球,观察颜色后放回袋中,同时放入2只与取出的球同色的球,这样连续取2次,则他取出的两只球中第1次取出的是白球,第2次取出的是黄球的概率是A.8/77B.4/21C.2/11D.4/7
袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球.以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求P{X=1|Z=0};(Ⅱ)求二维随机变量(X,Y)的概率分布.
袋中有l个红色球,2个黑色球与三个白球,现有放回地从袋中取两次,每次取一球,以 X,Y,Z分别表示丽次取球所取得的红球、黑球与白球的个数。 (1)求P{X=1|Z=0}; (2)求二维随机变量(X,Y)的概率分布。
袋子中有70个红球,30个黑球,从袋中任意摸出一个球,观察颜色后放回袋中,再摸第二个球,观察颜色后也放回袋中。(1)求两次摸球均为红球的概率;(3分)(2)求两次摸球颜色不同的概率。(4分)
一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中,直至取到红球,然后再取一球,假设每次取球时各个球被取到的可能性相同,求第一、第二次都取到红球的概率( )。A.7/10B.7/15C.7/20D.7/30
一个口袋中有7个红球3个白球,从袋中任取一任球,看过颜色后是白球则放回袋中,直至取到红球,然后再取一球,假设每次取球时各个球被取到的可能性相同,求第一、第二次都取到红球的概率( )。A.7/10B.7/15C.7/20D.7/30
填空题甲袋中有5只白球,5只红球,15只黑球,乙袋中有10只白球,5只红球,10只黑球,从两袋中各取一球,则两球颜色相同的概率为____。