对于高压同轴电缆,为了在外导体尺寸固定不变(半径b=定值)与外加电压不变(U0一定值)的情况下,使介质得到最充分利用,则内导体半径a的最佳尺寸应为外导体半径b的倍数是( )。
对于高压同轴电缆,为了在外导体尺寸固定不变(半径b=定值)与外加电压不变(U0一定值)的情况下,使介质得到最充分利用,则内导体半径a的最佳尺寸应为外导体半径b的倍数是( )。
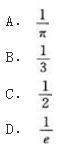
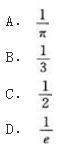
参考解析
解析:设同轴电缆的内导体单位长度所带电荷为τ,则电场强度为:

同轴电缆电压为U0(内外导体电位差)为:

解得:

代入电场强度公式,得到电场强度:

为使介质得到充分利用,即电场强度Er=a取得最大值。由于电容器承受最大电压U0一定,则当a(lnb-lna)取得极小值时,电场强度取得最大值。
根据题目已知条件及函数极值的求解方式,设b固定,对a求导可得:

由导数几何意义,当 f′(a)=0时,Er=a取得极值,则:

解得:


同轴电缆电压为U0(内外导体电位差)为:

解得:

代入电场强度公式,得到电场强度:

为使介质得到充分利用,即电场强度Er=a取得最大值。由于电容器承受最大电压U0一定,则当a(lnb-lna)取得极小值时,电场强度取得最大值。
根据题目已知条件及函数极值的求解方式,设b固定,对a求导可得:

由导数几何意义,当 f′(a)=0时,Er=a取得极值,则:

解得:

相关考题:
导体的电阻是导体本身的一种性质,对于同种材料的导体,下列表述正确的是A.横截面积一定,电阻与导体的长度成正比B.长度一定,电阻与导体的横截面积成正比C.电压一定,电阻与通过导体的电流成正比D.电流一定,电阻与导体两端的电压成反比
一圆柱形电容器,外导体的内半径为2cm,其间介质的击穿场强为200kV/cm,若其内导体的半径可以自由选择,则电容器能承受的最大电压为( )。 A. 284kV B. 159kV C. 252kV D. 147kV
一同轴电缆长L=2m,其内导体半径R1=1cm,外导体内半径为R2=6cm,导体间绝缘材料的电阻率ρ=1×109Ω·m。当内外导体间电压为500V时,绝缘层中漏电流为( )。A.3.51μAB.7.02μFC.1.76mAD.8.86mA
在一个圆柱形电容器中,置有两层同轴的圆柱体,其内导体的半径为2cm,外导体的内半径为8cm,内、外两绝缘层的厚度分别为2cm和4cm。内、外导体间的电压为150V(以外导体为电位参考点)。设有一根薄的金属圆柱片放在两层绝缘体之间,为了使两层绝缘体内的最大场强相等,金属圆柱片的电位应为:(A)100V (B)250V(C)667V (D)360V
以下有关同种材料导体电导说法正确的有()。A、当导体截面一定时,如果导体长度越短,导体的电导值则越小B、当导体长度一定时,如果导体截面越小,导体的电导值则越大C、当导体截面一定时,如果导体长度越长,导体的电导值则越小D、当导体长度一定时,如果导体截面越大,导体的电导值则越大
同轴电缆的特性阻抗取决于外导体的内径与内导体的外径之比,也就是说,同轴电缆外导体的内径和内导体的外径一定的话,电缆尺寸即使按比例扩大,其特性阻抗也仍保持定值,而射频电缆统一使用()系列是因为此时对射频信号衰减最小。A、75ΩB、50ΩC、100ΩD、300Ω
一同轴电缆长1=2m,其芯线导体半径r1=1cm,铅皮外壳内半径r2=6cm,导体间绝缘材料的电阻率ρ=1×109Ω*m,当内导体与外壳间电压U0为500V时,绝缘层中漏电流为()。A、8.86mAB、7.02μAC、3.51μAD、1.76mA
单选题一同轴电缆长1=2m,其芯线导体半径r1=1cm,铅皮外壳内半径r2=6cm,导体间绝缘材料的电阻率ρ=1×109Ω*m,当内导体与外壳间电压U0为500V时,绝缘层中漏电流为()。A8.86mAB7.02μAC3.51μAD1.76mA
判断题通电导体磁场强度的分布规律是:导体中心的磁场强度等于零,磁场强度随导体半径增加而增加,在导体表面有极大值A对B错