共用题干假设资本资产定价模型成立,相关证券的风险与收益信息如表3-6所示。(注:表中的数字是相互关联的)根据案例回答27~34题。根据资本资产定价模型理论(CAPM)的建议,一个资产分散状况良好的投资组合,最容易受()因素的影响。A:系统性风险B:投资分配比例C:证券种类的选择D:非系统性风险
共用题干
假设资本资产定价模型成立,相关证券的风险与收益信息如表3-6所示。(注:表中的数字是相互关联的)
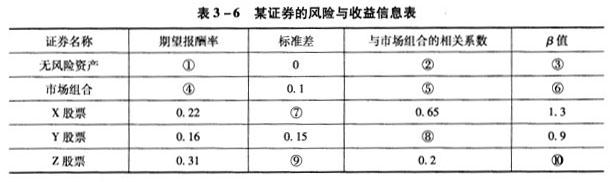
根据案例回答27~34题。
假设资本资产定价模型成立,相关证券的风险与收益信息如表3-6所示。(注:表中的数字是相互关联的)

根据案例回答27~34题。
根据资本资产定价模型理论(CAPM)的建议,一个资产分散状况良好的投资组合,最容易受()因素的影响。
A:系统性风险
B:投资分配比例
C:证券种类的选择
D:非系统性风险
A:系统性风险
B:投资分配比例
C:证券种类的选择
D:非系统性风险
参考解析
解析:一个资产分散状况良好的投资组合必定已很好地分散和消除了非系统性风险,因此非系统性风险对该投资组合的收益水平不会造成很明显的影响。但是系统性风险是无法消除的,它对该投资组合的收益水平有较大影响。
对于无风险资产来说,其市场风险β值为0,即不存在;从而可知其与市场组合的相关系数为0。
对于市场组合来说,其市场风险β值为1;从而可知其与本身的相关系数为1。
利用X股票和Y股票的数据解联立方程:0.22=无风险资产报酬率+1.3*(市场组合报酬率-无风险资产报酬率)0.16=无风险资产报酬率+0.9*(市场组合报酬率-无风险资产报酬率)可得:无风险资产报酬率=0.025;市场组合报酬率=0.175。
β=与市场组合的相关系数*(股票标准差/市场组合标准差),即:1.3=0.65*(X股票标准差/0.1),进而可得:X股票标准差=0.2。
根据β值的计算公式求Y股票的相关系数:0.9=r*(0.15/0.1),可得:r=0.6。
根据资本资产定价模型计算Z股票的β值:0.31=0.025+β*(0.175-0.025),可得:β=1.9。
根据β值的计算公式求z股票的标准差:1.9=0.2*(标准差/0.1),可得:标准差=0.95。
对于无风险资产来说,其市场风险β值为0,即不存在;从而可知其与市场组合的相关系数为0。
对于市场组合来说,其市场风险β值为1;从而可知其与本身的相关系数为1。
利用X股票和Y股票的数据解联立方程:0.22=无风险资产报酬率+1.3*(市场组合报酬率-无风险资产报酬率)0.16=无风险资产报酬率+0.9*(市场组合报酬率-无风险资产报酬率)可得:无风险资产报酬率=0.025;市场组合报酬率=0.175。
β=与市场组合的相关系数*(股票标准差/市场组合标准差),即:1.3=0.65*(X股票标准差/0.1),进而可得:X股票标准差=0.2。
根据β值的计算公式求Y股票的相关系数:0.9=r*(0.15/0.1),可得:r=0.6。
根据资本资产定价模型计算Z股票的β值:0.31=0.025+β*(0.175-0.025),可得:β=1.9。
根据β值的计算公式求z股票的标准差:1.9=0.2*(标准差/0.1),可得:标准差=0.95。