图示瞬时,作平面运动图形上A、B两点的加速度相等,即aA=aB,则该瞬时平面图形的角速度ω与角加速度α分别是:A. ω=0,α≠0B. ω≠0,α=0C. ω=0,α=0D.ω≠0,α≠0
图示瞬时,作平面运动图形上A、B两点的加速度相等,即aA=aB,则该瞬时平面图形的角速度ω与角加速度α分别是:
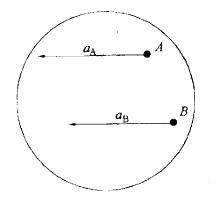

A. ω=0,α≠0
B. ω≠0,α=0
C. ω=0,α=0
D.ω≠0,α≠0
B. ω≠0,α=0
C. ω=0,α=0
D.ω≠0,α≠0
参考解析
解析:提示:求平面图形上一点加速度的基点法,aB=aA+aBAn+aBAτ。
相关考题:
刚体作平面运动,某瞬时平面图形的角速度为ω,角加速度为α,则其上任意两点A、B的加速度在A、B连线上投影的关系是:A.比相等B.相差AB * ω2C.相差AB * αD.相差(AB * ω2 + AB * α)
已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0,角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。A.指向O点B.垂直mn直线C.与mn直线成θ角D.沿mn直线背离O点
圆盘某瞬时以角速度ω,角加速度α绕O轴转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R,OB=R/2,则aA与aB,θ与φ的关系分别为:A.aA=aB,θ=φB. aA=aB,θ=2φC. aA=2aB,θ=φD. aA=2aB,θ=2φ
如图4-53所示,平面机构在图示位置时,杆AB水平而杆OA铅直,若B点的速度vB≠0,加速度aB=0。则此瞬时杆OA的角速度、角加速度分别为( )。A.ω=0,α≠0 B.ω≠0,α≠0 C.ω=0,α=0 D.ω≠0,α=0
如图4-45所示,圆盘某瞬时以角速度ω,角加速度α绕轴O转动,其上A、B两点的加速度分别为aA和aB,与半径的夹角分别为θ和φ。若OA=R, OB = R/2,则aA与aB,θ与 φ 的关系分别为( )。A.aA=aB θ=φ B.aA=aB θ=2φ C.aA=2aB θ=φ D.aA=2aB θ=2φ
平面图形在其平面内运动,某瞬时其上有两点的加速度矢相同,则下述正确的有()A、其上各点速度在该瞬时一定都相等B、其上各点加速度在该瞬时一定都相等C、其上各点速度在该瞬时一定不相等D、其上各点加速度在该瞬时一定不相等
平面图形在其平面内运动,某瞬时其上有两点的加速度相等,则()A、其上各点速度在该瞬时一定都相等B、其上各点加速度在该瞬时一定都相等C、该图形在此瞬时一定作平动D、该平面图形在此瞬时角速度可能不为零,但角速度一定为零
平面图形在其自身平面内运动,其上有两点速度矢在某瞬时相同,以下四种说法,哪些是正确的?()A、在该瞬时,其上各点的速度都相等;B、在该瞬时,其上各点的加速度都相等;C、在该瞬时,图形的角加速度一定为零,但角速度不一定为零;D、在该瞬时,图形的角速度一定为零,但角加速度不一定为零。
平面图形在其自身平面内运动,以下四种说法中,哪些是正确的?()A、若其上有两点的速度为零,则此瞬时其上所有各点的速度一定都为零;B、若其上有两点的速度在这两点连线的垂线(垂线也在此平面内)上的投影的大小相等,则此瞬时其上所有各点的速度的大小和方向都相等;C、若其上有两点的速度矢量之差为零,则此瞬时该平面图形一定是作瞬时平移或平移运动;D、其上任意两点的加速度在这两点的连线上的投影一定相等。
单选题刚体作平面运动,某瞬时平面图形的角速度为w,角加速度为α,则其上任意两点A、B的加速度在A、B连线上投影的关系是:()A 比相等B 相差AB·w2C 相差AB·αD 相差(AB·w2+AB·α)