阅读以下说明和流程图,填补流程图和问题中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】设整型数组A[1:N]每个元素的值都是1到N之间的正整数。一般来说,其中会有一些元素的值是重复的,也有些数未出现在数组中。下面流程图的功能是查缺查重,即找出A[1:N]中所有缺的或重复的整数,并计算其出现的次数(出现次数为0时表示缺)。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1:N]加上的一个映射,并用数组C[1:N]记录各整数出现的次数,需输出所有缺少的或重复的数及其出现的次数。【流程图】【问题】 如果数组A[1:5]的元素分别为{3,2,5,5,1},则算法流程结束后输出结果为: (5) 输出格式为:缺少或重复的元素,次数(0表示缺少)
阅读以下说明和流程图,填补流程图和问题中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】设整型数组A[1:N]每个元素的值都是1到N之间的正整数。一般来说,其中会有一些元素的值是重复的,也有些数未出现在数组中。下面流程图的功能是查缺查重,即找出A[1:N]中所有缺的或重复的整数,并计算其出现的次数(出现次数为0时表示缺)。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1:N]加上的一个映射,并用数组C[1:N]记录各整数出现的次数,需输出所有缺少的或重复的数及其出现的次数。【流程图】
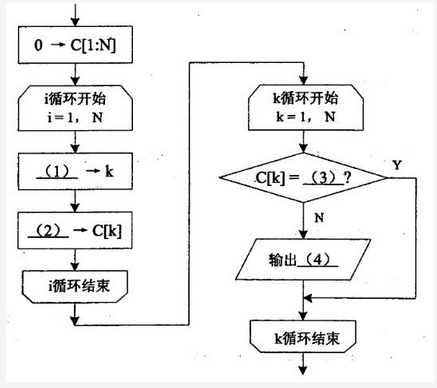
【问题】 如果数组A[1:5]的元素分别为{3,2,5,5,1},则算法流程结束后输出结果为: (5) 输出格式为:缺少或重复的元素,次数(0表示缺少)

【问题】 如果数组A[1:5]的元素分别为{3,2,5,5,1},则算法流程结束后输出结果为: (5) 输出格式为:缺少或重复的元素,次数(0表示缺少)
参考解析
解析:(1)A[i](2)C[k]+1(3)1(4)k和C[k](5)4,{1,1,1,0,2}
【解析】
(1)A[i](2)C[k]+1(3)1(4)k和C[k](5)4,{1,1,1,0,2}
【解析】
(1)A[i](2)C[k]+1(3)1(4)k和C[k](5)4,{1,1,1,0,2}
相关考题:
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较“K(I)+K(J):M”最少执行次数约为(5)。
阅读以下说明和流程图,回答问题将解答填入对应栏。[说明]本流程图实现采用递归函数来求一个整数数组中从元素0到元素n中的最小值。该算法思想是这样的,首先我们假设有一个求数组中最小元素的函数,然后,在求某一具有n的元素的数组的最小值时,只要求将前n-1的元素的最小值与第n个元素比较即可。不断地重复这一过程,直到数组中只剩下一个元素,那么它必定是最小值。注:int min(int X,int y)为返回两数中最小数的函数。int minInArray(int a[],int n)为返回数组中最小数的函数。minA为数组中最小值。[问题l]将流程图的(1)~(4)处补充完整。[问题2]min()函数的定义为(5)。
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)~(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。【流程图】
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。【说明】假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】有数组A(4,4),把1到16个整数分别按顺序放入A(1,1),…,A(1,4),A(2,1),…,A(2,4),A(3,1),…,A(3,4),A(4,1),…,A(4,4)中,下面的流程图用来获取数据并求出两条对角线元素之积。【流程图】
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】对于大于1的正整数n,(x+1)n可展开为下面流程图的作用是计算(x+1)n展开后的各项系数(i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x+1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,和都为1,因此可直接设置A[0]、A[k]的值为1。 例如,计算(x+1)3的过程如下:先计算(x+1)2(即k=2)的各项系数,然后计算(x+1)3(即k=3)的各项系数。K=2时,需要计算,和,并存入A[0],A[1]和A[2],其中A[0]和A[1]的值已有,因此将(即A[1])和即(A[0])相加得到的值并存入A[1]。k=3时,需要计算,和和,先计算出(由)得到并存入A[2],再计算(由得到)并存入A[1]。
阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入对应栏内。[说明]下面的流程图旨在统计指定关键词在某一篇文章中出现的次数。设这篇文章由字符A(0),…,A(n-1)依次组成,指定关键词由字符B(0),…,B(m-1)依次组成,其中,n>m≥1。注意,关键词的各次出现不允许有交叉重叠。例如,在“aaaa”中只出现两次“aa”。该流程图采用的算法是:在字符串A中,从左到右寻找与字符串B相匹配的并且没有交叉重叠的所有子串。流程图中,i为字符串A中当前正在进行比较的动态予串首字符的下标,j为字符串B的下标,k为指定关键词出现的次数。[流程图]
阅读以下说明和流程图,回答问题1-2,将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法,实现了计算两正整数最大公约数的功能。给定正整数m和 n,假定m大于等于n,算法的主要步骤为:(1)以n除m并令r为所得的余数;(2)若r等于0,算法结束;n即为所求;(3)将n和r分别赋给m和n,返回步骤(1)。[流程图][问题1] 将流程图中的(1)~(4)处补充完整。[问题2] 若输入的m和n分别为27和21,则A中循环体被执行的次数是(5)。
阅读下列说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左到右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数X相等的数。如果找不到则输出false;只要找到一个(可能有多个)就输出True以及该元素的下标i和j(注意数组元素的下标从1开始)。 例如,在如下矩阵中查找整数8,则输出伟:True,4,1 2 4 6 9 4 5 9 10 6 7 10 12 8 9 11 13 流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数X进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.O(m*n) D,O(m+n)
试题一(共15分)阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】两个包含有限个元素的非空集合A、B的相似度定义为IAUBI/IA U Bl,即它们的交集大小(元素个数)与并集大小之比。以下的流程图计算两个非空整数集合(以数组表示)的交集和并集,并计算其相似度。己知整数组A[1:m】和B【1:n】分别存储了集合A和B的元素(每个集合中包含的元素各不相同),其交集存放于数组C[1:s】,并集存放于数组D【1:t】,集合A和B的相似度存放于SIM。例如,假设A={1,2,3,4},B={1,4,5,6},则C={1,4},D={1,2,3,4,5,6},A与B的相似度SIM=1/3。
?????? 阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)li=l,…,n}(n>1)}.其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)[j=l,…,m},而每个关键词K(j)出现的次数为NK(j).j=l,…,m。??????
●试题二阅读下列说明、流程图和算法,将应填入(n)处的字句写在答题纸的对应栏内。【说明】下面的流程图(如图3所示)用N-S盒图形式描述了数组A中的元素被划分的过程。其划分方法是:以数组中的第一个元素作为基准数,将小于基准数的元素向低下标端移动,而大于基准数的元素向高下标端移动。当划分结束时,基准数定位于A[i],并且数组中下标小于i的元素的值均小于基准数,下标大于i的元素的值均大于基准数。设数组A的下界为low,上界为high,数组中的元素互不相同。例如,对数组(4,2,8,3,6),以4为基准数的划分过程如下:【流程图】图3流程图【算法说明】将上述划分的思想进一步用于被划分出的数组的两部分,就可以对整个数组实现递增排序。设函数int p(int A[],int low,int high)实现了上述流程图的划分过程并返回基准数在数组A中的下标。递归函数void sort(int A[],int L,int H)的功能是实现数组A中元素的递增排序。【算法】void sort (int A[], int 1,int H){if ( LH){k=p(A,L,R);//p()返回基准数在数组A中的下标sort( (4) );//小于基准数的元素排序sort( (5) );//大于基准数的元素排序}}
●试题一阅读下列说明和流程图,将应填入(n)处的语句写在答题纸的对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。图1
试题一(共 15 分)阅读以下说明和流程图,填补流程图中的空缺(1)~(9) ,将解答填入答题纸的对应栏内。[说明]假设数组 A 中的各元素 A(1),A(2) ,…,A(M)已经按从小到大排序(M≥1) ;数组 B 中的各元素 B(1),B(2),…,B(N)也已经按从小到大排序(N≥1) 。执行下面的流程图后, 可以将数组 A 与数组 B 中所有的元素全都存入数组 C 中, 且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序) 。例如,设数组 A 中有元素:2,5,6,7,9;数组B 中有元素:2,3,4,7;则数组 C 中将有元素:2,2,3,4,5,6,7,7,9。[流程图]
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。[说明]两个包含有限个元素的非空集合A、B的相似度定义为|A∩B|/|A∪B|,即它们的交集大小(元素个数)与并集大小之比。以下的流程图计算两个非空整数集合(以数组表示)的交集和并集,并计算其相似度。已知整数组A[1:m]和B[1:n]分别存储了集合A和B的元素(每个集合中包含的元素各不相同),其交集存放于数组C[1:s],并集存放于数组D[1:t],集合A和B的相似度存放于SIM。例如,假设A={1,2,3,4},B={1,4,5,6},则C={1,4),D={1,2,3,4,5,6},A与B的相似度SIM=1/3。[流程图]
阅读下列说明和流程图,填补流程图中的空缺(1)~(9),将解答填入答题纸的对应栏内。【说明】假设数组A中的各元素A⑴,A (2),…,A (M)已经按从小到大排序(M>1):数组B中的各元素B(1) , B (2) . B (N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序(注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素: 2,5,6,7,9;数组B中有元素: 2,3,4,7;则数组C中将有元素: 2,2,3,4,5,6,7,7,9.
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。[说明]本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n>1)},其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)|j=1,…,m},而每个关键词K(j)出现的次数为NK(j),j=1,…,m。[流程图]
阅读以下说明和流程图,填补流程图中的空缺(1)~(9),将解答填入对应栏内。1、【说明】 假设数组A中的各元素A(1),A(2),…,A(M)已经按从小到大排序(M≥1);数组B中的各元素B(1),B(2),…,B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后,可以将数组A与数组B中所有的元素全都存入数组C中,且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序)。例如,设数组A中有元素:2,5, 6,7,9;数组B中有元素2,3,4,7:则数组C中将有元素:2,2,3,4,5,6,7, 7, 9。【流程图】
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。[说明]下面的函数sort(int n,int a[])对保存在数组a中的整数序列进行非递减排序。由于该序列中的元素在一定范围内重复取值,因此排序方法是先计算出每个元素出现的次数并记录在数组b中,再从小到大顺序地排列各元素即可得到一个非递减有序序列。例如,对于序列6,5,6,9,6,4,8,6,5,其元素在整数区间[4,9]内取值,因此使数组元素b[0]~b[5]的下标0~5分别对应数值4~9,顺序地扫描序列的每一个元素并累计其出现的次数,即将4的个数记入b[0],5的个数记入b[1],依此类推,9的个数记入b[5]。最后依次判断数组b的每个元素值,并将相应个数的数值顺序地写入结果序列即可。对于上例,所得数组b的各个元素值如下:1.jpg那么在输出序列中写入1个4、2个5、4个6、1个8、1个9,即得4,5,5,6,6,6,6,8,9,从而完成排序处理。[C函数] void sort(int n,int a[]) { int *b; int i, k, number; int minimum=a[0],maximum=a[0]; /*minimum和maximum分别表示数组a的最小、最大元素值*/ for(i=1; i<n; i++){ if(______) minimum=a[i]; eiSe if (______) maximum=a[i]; } number=maximum-minimum+1; if(number<=i)return; b=(int*)calloc(number,sizeof(int)); if(!b) return; for(i=0;i<n; i++){/*计算数组a的每个元素值出现的次数并记入数组b */ k=a[i]-minimum; ++b[k]; } /*按次序在数组a中写入排好的序列*/ i=______; for(k=0; k<number; k++) for(; ______; --b[k] ) a[i++]=minimum+______; }
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】如果n位数(n≧2)是回文数(从左到右读与从右到左读所得结果一致),且前半部分的数字递增(非减)、后半部分的数字将递减(非增),则称该数为拱形回文数。例如,12235753221 就是一个拱形回文数。显然,拱形回文数中不含数字0。下面的流程图用于判断给定的n位数(各位数字依次存放在数组的各个元素A[ i ]中,i =1,2,…,n)是不是拱形回文数。流程图中,变量T 动态地存放当前位之前一位的数字。当n 是奇数时,还需要特别注意中间一位数字的处理。【流程图】注1:“循环开始”框内给出的循环控制变量的初值、终值和增值(默认为1),格式为:循环款控制变量=初值,终值[ , 增值 ]注2:函数int(x)为取x的整数部分,即不超过x 的最大整数。
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。[说明]下面流程图的功能是:在给定的一个整数序列中查找最长的连续递增子序列。设序列存放在数组A[1:n](n≥2)中,要求寻找最长递增子序列A[K:K+L-1](即A[K]<A[K+1]<…<A[K+L-1])。流程图中,用Kj和Lj分别表示动态子序列的起始下标和长度,最后输出最长递增子序列的起始下标K和长度L。例如,对于序列A={1,2,4,4,5,6,8,9,4,5,8},将输出K=4,L=5。[流程图] 注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
试题(15 分)阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏 内。【说明】设有整数数组 A[1:N](N>1),其元素有正有负。下面的流程图在该数组 中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标 K、元素 个数 L 以及最大的和值 M。例如,若数组元素依次为 3,-6,2,4,-2,3,-1,则输出 K=3,L=4,M=7。 该流程图中考察了 A[1:N]中所有从下标 i 到下标 j(j≥i)的各元素之和 S,并动态地记录其最大值 M。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为 1,格式为:循环控制变量=初值,终值
第一题 阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】对于大于1的正整数n,(x+1)n可展开为问题:1.1 【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。格式为:循环控制变量=初值,终值,递增值。
试题一(共 20 分)阅读下列说明和图,回答问题 1 至问题 3,将解答填入答题纸的对应栏内。【说明】设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左至右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数 X 相等的数。如果找不到则输出“false”;只要找到一个(可能有多个)就输出“True”以及该元素的下标 i 和 j(注意数组元素的下标从 1 开始)。例如,在如下矩阵中查找整数 8,则输出伟:True,4,12 4 6 94 5 9 106 7 10 128 9 11 13流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数 X 进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】【问题】该算法的时间复杂数是()供选择答案:A.O(1) B.O(m+n) C.(m*n) D,O(m2+n2)
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】设有整数数组A[1:N](N>1),其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大的和值M。例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)的各元素之和S,并动态地记录其最大值M。【流程图】注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值