采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i-1个整数已经排好序,将第i个整数依次和第i-1,i-2,…个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5,2,4,6,1,3}进行从小到大排序,则需要进行( )次整数之间的比较。对于该排序算法,输入数据具有(请作答此空)特点时,对整数进行从小到大排序,所需的比较次数最多。A.从小到大B.从大到小C.所有元素相同D.随机分布
采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i-1个整数已经排好序,将第i个整数依次和第i-1,i-2,…个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5,2,4,6,1,3}进行从小到大排序,则需要进行( )次整数之间的比较。对于该排序算法,输入数据具有(请作答此空)特点时,对整数进行从小到大排序,所需的比较次数最多。
A.从小到大
B.从大到小
C.所有元素相同
D.随机分布
B.从大到小
C.所有元素相同
D.随机分布
参考解析
解析:采用插入排序算法对6个整数{5,2,4,6,1,3}进行从小到大排序的过程如表所示。
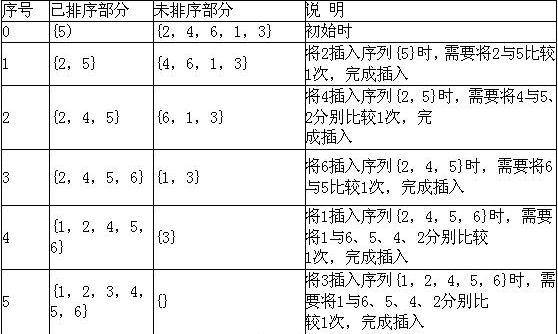
综上,元素间共比较12次。从上表中的第4步可看出,当待插入的元素比已排序部分的所有元素都要小时,需要比较和移动的元素最多,因此当输入数据序列正好从大到小排列,而需要将其从小到大排序时,元素间的比较次数最多。

综上,元素间共比较12次。从上表中的第4步可看出,当待插入的元素比已排序部分的所有元素都要小时,需要比较和移动的元素最多,因此当输入数据序列正好从大到小排列,而需要将其从小到大排序时,元素间的比较次数最多。
相关考题:
●下面算法是实现对n个整数的序列进行选择排序,其中序列的"长度"n为问题的规模。该算法的时间复杂度为 (23) 。void select_sort(int a[],int n){//将a中整数序列重新排列成从小到大有序的整数序列for(i=0;in-1;++i){j=i;for(k=i+1;kn;++k)if(a[k]a[j])j=k;if(j!=i){w=a[j];a[j]=a[i];a[i]=w;}}//select- sort(23) A.O(n3)B.O(n2)C.O(n)D.O(n4)
● 对于具有n 个元素的一个数据序列,若只得到其中第 k 个元素之前的部分排序, 最好采用(59) ,使用分治 (Divide and Conquer )策略的是(60) 算法。(59)A. 希尔排序 B. 直接插入排序 C. 快速排序 D. 堆排序(60)A. 冒泡排序 B. 插入排序 C. 快速排序 D. 堆排序
下面算法是实现对n个整数的序列进行选择排序,其中序列的“长度”n为问题的规模。该算法的时间复杂度为(11)。 void select_sort(int a[],int n){ //将a中整数序列重新排列成从小到大有序的整数序列 for(i=0;i<n-1;++i){ j=i; for(k=i+1;k<n;++k)if(a[k]<a[j])j=k; if(j!=i){w=a[j];a[j];a[i];a[i]=w} )//select_sortA.O(n2)B.O(n3)C.O(n4)D.O(n)
●用插入排序和归并排序算法对数组3,1,4,1,5,9,6,5进行从小到大排序,则分别需要进行 (65) 次数组元素之间的比较。(65)A.12,14B.10,14C.12,16D.10,16
对n个关键码构成的序列采用直接插入排序法进行升序排序的过程是:在插入第i个关键码Ki时,其前面的i-1个关键码己排好序,因此令Ki与Ki-1、Ki-2、...,依次比较,多到K1为止,找到插入位置并移动相关元素后将Ki插入有序子序列的适当位置,完成本趟(即第i-1趟)排序。以下关于直接插入排序的叙述中,正确的是()。A.若原关键码序列已经升序排序,则排序过程中关键码间的比较次数最少B.若原关键码序列已经降序排序,则排序过程中关键码间的比较次数最少C.第1趟完成后即可确定整个序列的最小关键码D.第1趟完成后即可确定整个序列的最大关键码
对n个基本有序的整数进行排序,若采用插入排序算法,则时间和空间复杂度分别为(62);若采用快速排序算法,则时间和空间复杂度分别为(63)。A.O(n2)和O(n)B.O(n)和O(n)C.O(n2)和O(1)D.O(n)和O(1)
采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i-1个整数己经排好序,将第i个整数依次和第i-1, i-2, ...个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5.2.4.6.1.3}进行从小到大排序,则需要进行(31)次整数之间的比较。对于该排序算法,输入数据具有(32)特点时,对整数进行从小到大排序,所需的比较次数最多。A.9B.10C.12D.13
已知一个单链表中有3000个结点,每个结点存放一个整数,( )可用于解决这3000个整数的排序问题且不需要对算法作大的变动。A.直接插入排序方法B.简单选择排序方法C.快速排序方法D.堆排序方法
采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i一1个整数已经排好序,将第i个整数依次和第i.,i-2,…个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5 2,4,6,1,3}进行从小到大排序,则需要进行(31)次整数之间的比较。对于该排序算法,输入数据具有(32)特点时,对整数进行从小到大排序,所需的比较次数最多。A.9B.10C.12D.13(32)A.从小到大B.从大到小C.所有元素相同D.随机分布请帮忙给出每个问题的正确答案和分析,谢谢!
采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i-1个整数已经排好序,将第i个整数依次和第i-1,i-2,…个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5,2,4,6,1,3}进行从小到大排序,则需要进行(请作答此空)次整数之间的比较。对于该排序算法,输入数据具有( )特点时,对整数进行从小到大排序,所需的比较次数最多。A. 9B. 10C. 12D. 13
阅读以下说明和代码,填补代码中的空缺,将解答填入答题纸的对应栏内。【说明】下面的程序利用快速排序中划分的思想在整数序列中找出第 k 小的元素(即 将元素从小到大排序后,取第 k 个元素)。对一个整数序列进行快速排序的方法是:在待排序的整数序列中取第一个数 作为基准值,然后根据基准值进行划分,从而将待排序的序列划分为不大于基准 值者(称为左子序列)和大于基准值者(称为右子序列),然后再对左子序列和 右子序列分别进行快速排序,最终得到非递减的有序序列。例如,整数序列“19, 12, 30, 11,7,53, 78, 25"的第 3 小元素为 12。整数序列“19, 12,7,30, 11, 11,7,53. 78, 25, 7"的第 3 小元素为 7。函数 partition(int a[], int low,int high)以 a[low]的值为基准,对 a[low]、 a[low+l]、…、a[high]进行划分,最后将该基准值放入 a[i] (low≤i≤high),并 使得 a[low]、a[low+l]、,..、A[i-1]都小于或等于 a[i],而 a[i+l]、a[i+2]、..、 a[high]都大于 a[i]。函 教 findkthElem(int a[],int startIdx,int endIdx,inr k) 在 a[startIdx] 、 a[startIdx+1]、...、a[endIdx]中找出第 k 小的元素。【代码】#include #include Int partition(int a [],int low, int high){//对 a[low..high]进行划分,使得 a[low..i]中的元素都不大于 a[i+1..high]中的 元素。int pivot=a[low]; //pivot 表示基准元素 Int i=low,j=high;while(( 1) ){While(ipivot)--j; a[i]=a[ j] While(ipivot)++i; a[ j]=a[i]}(2) ; //基准元素定位 return i;}Int findkthElem(int a[],int startIdx,int endIdx, int k){//整数序列存储在 a[startldx..endldx]中,查找并返回第 k 小的元素。if (startldxendIdx || kendIdx||k-1 if (loc==k-1) ∥找到第 k 小的元素return (3) ;if(k-l 小的元素}return 0;}
阅读以下说明和C代码,填写程序中的空(1)~(5),将解答写入答题纸的对应栏内。【说明】直接插入排序是一种简单的排序方法,具体做法是:在插入第i个关键码时,k1,k2,…,ki-1已经排好序,这时将关键码ki依次与关键码ki-1,ki-2,…,进行比较,找到ki应该插入的位置时停下来,将插入位置及其后的关键码依次向后移动,然后插入ki。例如,对{17,392,68,36}按升序作直接插入排序时,过程如下:第1次:将392(i=1)插入有序子序列{17},得到{17,392};第2次:将68(i=2)插入有序子序列{17,392},得到{17,68,392};第3次:将36(i=3)插入有序子序列{17,68,392},得到{17,36,68,392},完成排序。下面函数 insertSort用直接插入排序对整数序列进行升序排列,在main函数中调用insertSort并输出排序结果。 【C代码】void insert Sort(int data[],int n)/*用直接插入排序法将data[0]~ data[n-1]中的n个整数进行升序排列*/{ int i,j; int tmp; for(i=1; i=0 j----) //查找插入位置并将元素后移 (2); (3) =tmp; //插入正确位置 }/*if*/ }/*for*/}/*insertSort*/ int main(){ int *bp,*ep; int n,arr[]={17,392,68,36,291,776,843,255}; n = sizeof(arr) / sizeof(int); insertSort(arr,n); bp= (4) ; ep = arr+n; for( ;bp=0 j----) //查找插入位置并将元素后移 (2); (3) =tmp; //插入正确位置 }/*if*/ }/*for*/}/*insertSort*/ int main(){ int *bp,*ep; int n,arr[]={17,392,68,36,291,776,843,255}; n = sizeof(arr) / sizeof(int); insertSort(arr,n); bp= (4) ; ep = arr+n; for( ;bp
对n个关键码构成的序列采用直接插入排序法进行升序排序的过程是:在插入第i个关键码Ki时,其前面的i-1个关键码己排好序,因此令Ki与Ki-1、Ki-2、...,依次比较,最多到K1为止,找到插入位置并移动相关元素后将Ki插入有序子序 列的适当位置,完成本趟(即第i-1趟)排序。以下关于直接插入排序的叙述中,正确的是( )。 A. 若原关键码序列已经升序排序,则排序过程中关键码间的比较次数最少 B.若原关键码序列已经降序排序,则排序过程中关键码间的比较次数最少 C.第1趟完成后即可确定整个序列的最小关键码 D.第1趟完成后即可确定整个序列的最大关键码
给定包含n个正整数的数组A和正整数x,要判断数组A中是否存在两个元素之和等于x,先用插入排序算法对数组A进行排序,再用以下过程P来判断是否存在两个元素之和等于x。low=1;high=n;while(high>low)if A[low]+A[high]=x return true;else if A[low]+A[high]>x low++;else high--;return false;则过程P的时间复杂度为( ),整个算法的时间复杂度为(请作答此空)。A.O(n)B.O(nlgn)C.O(n2)D.O(n2lgn)
采用插入排序算法对n个整数排序,其基本思想是:在插入第i个整数时,前i-1个整数己经排好序,将第i个整数依次和第i-1,i-2,...个整数进行比较,找到应该插入的位置。现采用插入排序算法对6个整数{5,2,4,6,1,3}进行从小到大排序,则需要进行( )次整数之间的比较。A.9B.10C.12D.13
排序算法中,从尚未排序序列中依次取出元素与已排序序列(初始为空)中的元素进行比较(要求比较次数尽量少),然后将其放入已排序序列的正确位置的方法是()A、折半插入排序B、直接插入排序C、归并排序D、选择排序
单选题排序算法中,从尚未排序序列中依次取出元素与已排序序列(初始为空)中的元素进行比较(要求比较次数尽量少),然后将其放入已排序序列的正确位置的方法是()A折半插入排序B直接插入排序C归并排序D选择排序
单选题若对n个元素进行直接插入排序,在进行第i趟排序时,假定元素r[i+1]的插入位置为r[j],则需要移动元素的次数为()。Aj-iBi-j-1Ci-jDi-j+1